通過交流電感器對電流流動的阻礙稱為感抗，它線性地取決于電源頻率。

當連接到交流電源時，流過電感線圈的電流會產生一個自感電動勢，該電動勢與最初建立電流的電動勢相反。對于包含交流電感的時間變化電路，電感線圈作為阻抗，限制了線圈中時間變化電流的流動。

電感器和扼流圈基本上是由導線繞成的線圈或環，要么繞在空心管上（空氣芯），要么繞在某種鐵磁材料上（鐵芯），以增加其電感值，稱為電感。

電感器以磁場的形式存儲能量，當電壓施加到電感器的端子上時，磁場被創建。通過電感器的電流增長不是瞬時的，而是由電感器自身的自感或反電動勢值決定的。對于電感線圈，這個反電動勢電壓VL與通過它的電流變化率成正比。

這個電流將繼續上升，直到達到其最大穩態條件，大約在五個時間常數時，這個自感反電動勢衰減到零。此時，穩態電流流過線圈，不再有反電動勢產生來阻礙電流流動，因此，線圈更像是一個短路，允許最大電流流過它。

然而，在包含交流電感的交流電路中，通過電感器的電流流動與穩態直流電壓下的行為非常不同。在交流電路中，通過線圈繞組的電流流動的阻礙不僅取決于線圈的電感，還取決于所施加電壓波形的頻率，因為它從正值變為負值。

在交流電路中，通過線圈的電流流動的實際阻礙由線圈的交流電阻決定，這個交流電阻由一個復數表示。但是為了區分直流電阻值和交流電阻值，后者也被稱為阻抗，使用術語“電抗”。

與電阻一樣，電抗以歐姆為單位測量，但用符號“X”來區分它與純電阻“R”值，并且由于所討論的組件是電感器，電感器的電抗稱為感抗（XL），以歐姆為單位測量。其值可以從公式中找到。

感抗

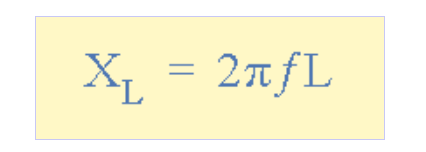
感抗

其中：

XL = 感抗，單位為歐姆（Ω）

π（pi）= 數值常數3.142

? = 頻率，單位為赫茲（Hz）

L = 電感，單位為亨利（H）

我們也可以用弧度來定義感抗，其中歐米茄，ω等于2π?。

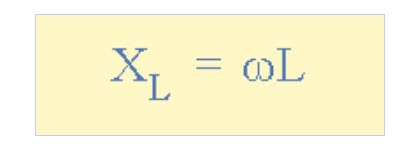
交流電感值

因此，每當正弦電壓施加到電感線圈時，反電動勢阻礙了通過線圈的電流的上升和下降，在具有零電阻或損耗的純電感線圈中，這個阻抗（可以是一個復數）等于其感抗。此外，電抗由矢量表示，因為它既有大小又有方向（角度）。考慮下面的電路。

帶有正弦電源的交流電感

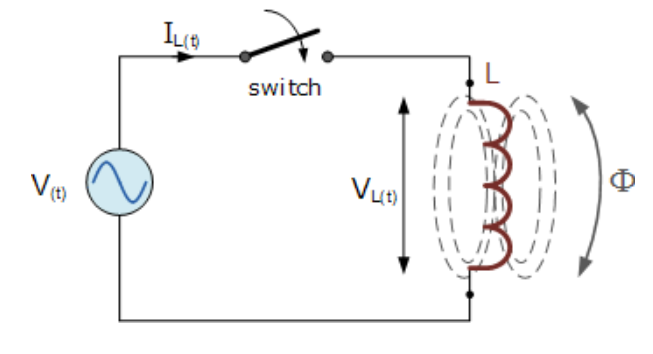
交流電感

上面的簡單電路由一個純電感L亨利（H）組成，連接到一個由表達式給出的正弦電壓：V(t) = Vmax sin ωt。當開關閉合時，這個正弦電壓將導致電流流動并從零上升到其最大值。這個電流的上升或變化將在線圈內感應出一個磁場，該磁場又將阻礙或限制這個電流的變化。

但在電流有時間達到其在直流電路中的最大值之前，電壓改變極性，導致電流改變方向。這個方向的改變再次被線圈中的自感反電動勢延遲，在僅包含純電感的電路中，電流被延遲了90度。

所施加的電壓在電流達到其最大正值之前四分之一（1/4?）周期達到其最大正值，換句話說，施加到純電感電路的電壓“領先”電流四分之一周期或90度，如下所示。

交流電感的正弦波形

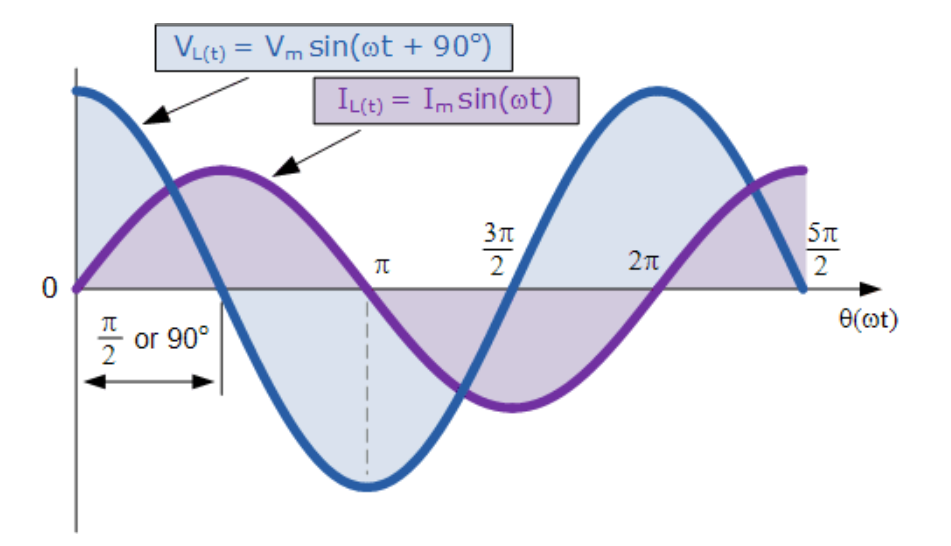
交流電感波形

這種效應也可以用相量圖表示，在純電感電路中，電壓“領先”電流90度。但是通過使用電壓作為我們的參考，我們也可以說電流“滯后”電壓四分之一周期或90度，如下面的矢量圖所示。

交流電感的相量圖

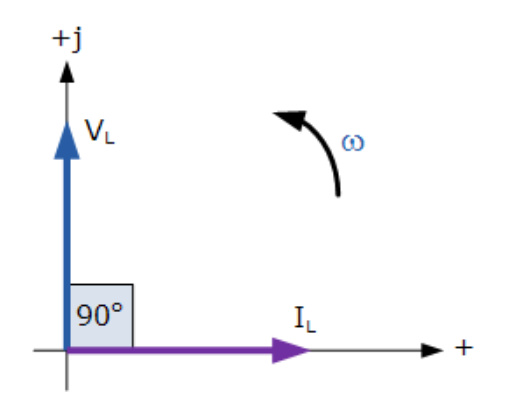
交流電感的相量圖

因此，對于純無損耗電感器，VL“領先”IL 90度，或者我們可以說IL“滯后”VL 90度。

有許多不同的方法可以記住通過純電感電路的電壓和電流之間的相位關系，但一種非常簡單且易于記憶的方法是使用助記符表達式“ELI”（發音為女孩名字Ellie）。

ELI代表在交流電感中電動勢先于電流I，L在I之前。換句話說，在電感器中電壓先于電流，E，L，I等于“ELI”，無論電壓從哪個相位角開始，這個表達式對于純電感電路始終成立。

頻率對感抗的影響

當50Hz的電源連接到合適的交流電感時，電流將如前所述延遲90度，并在每個半周期結束時電壓反轉極性之前達到I安培的峰值，即電流在“T秒”內上升到其最大值。

如果我們現在向線圈施加相同峰值電壓的100Hz電源，電流仍將延遲90度，但其最大值將低于50Hz的值，因為由于頻率的增加，達到其最大值所需的時間減少了，因為現在它只有“1/2 T秒”來達到其峰值。此外，由于頻率的增加，線圈內磁通量的變化率也增加了。

然后從上述感抗方程可以看出，如果頻率或電感增加，線圈的總感抗值也會增加。隨著頻率增加并接近無窮大，電感器的感抗及其阻抗也會增加，表現得像開路。

同樣，當頻率接近零或直流時，電感器的感抗也會降低到零，表現得像短路。這意味著感抗“與頻率成正比”，在低頻時值較小，在高頻時值較大，如圖所示。

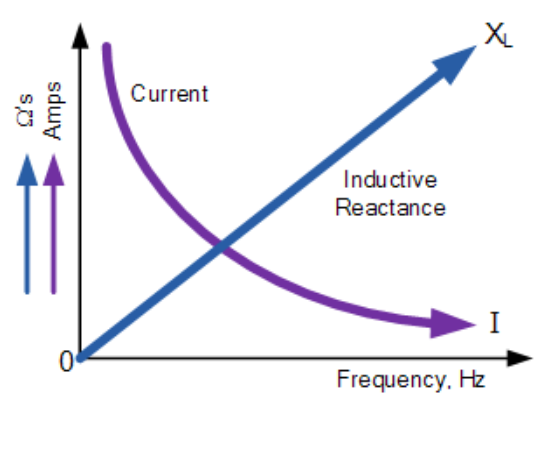
感抗與頻率的關系

感抗隨頻率增加而增加，因此感抗與頻率成正比（XL α ?），因為電感器中產生的反電動勢等于其電感乘以電感器中電流的變化率。

此外，隨著頻率的增加，通過電感器的電流值也會減少。

我們可以將極低和極高頻率對純交流電感感抗的影響表示如下：

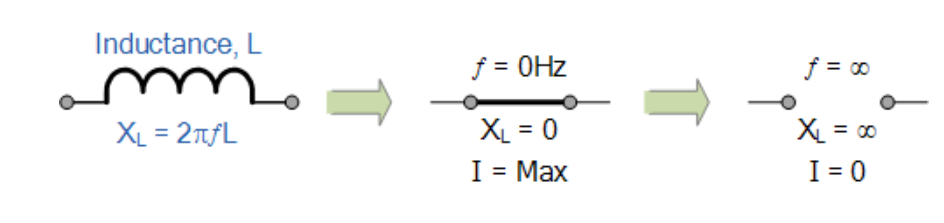
頻率對交流電感的影響

在包含純電感的交流電路中，適用以下公式：

通過交流電感的電流

那么，我們是如何得出這個方程的呢？電感器中的自感電動勢由法拉第定律決定，該定律產生“自感”效應。當電流通過電感線圈時，交流電流的變化率在同一線圈中感應出一個電動勢，該電動勢與變化的電流相反。線圈中由其自身磁場產生的效應，該磁場由通過它的電流流動產生，被任何電流變化所反對，稱為“自感”。

這個自感電動勢的最大電壓值將對應于電流變化的最大速率，線圈上的電壓值如下：

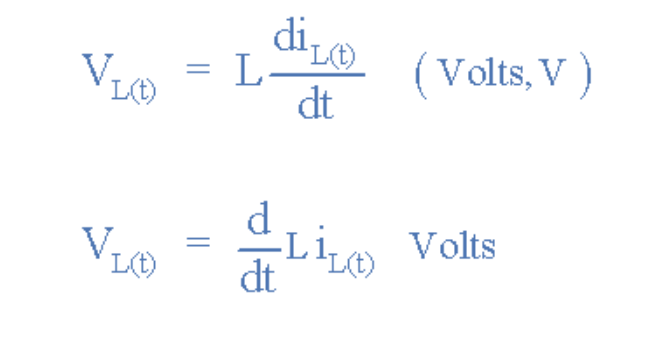
交流電感上的電壓

其中：d/dt表示電流隨時間的變化率。

通過電感線圈（L）的正弦電流在其周圍產生磁通量，如下所示：

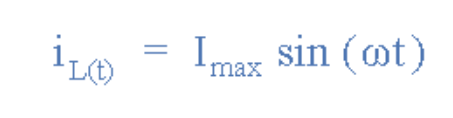
正弦電流

然后，上述方程可以重寫為：

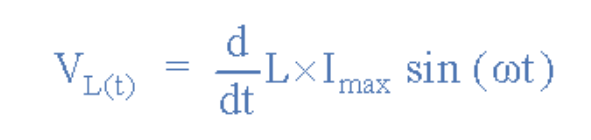
感應電壓

對正弦電流進行微分得到：

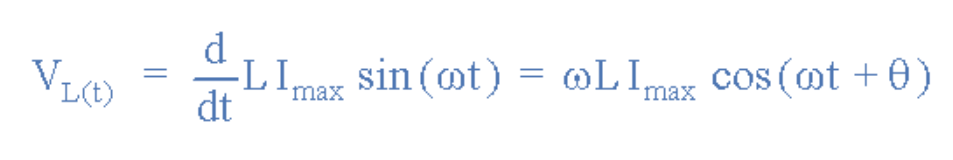
微分正弦電流

余弦波波形的三角恒等式c°s (ωt + 0°) = sin (ωt + 0° + 90°)實際上是一個正弦波形，偏移了+90°。然后，我們可以將上述方程重寫為正弦波形式，以定義交流電感上的電壓為：

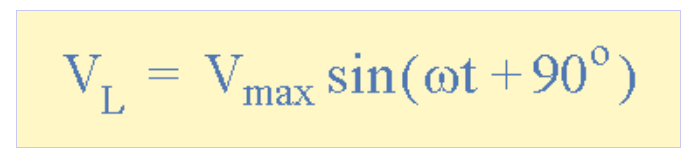
交流電感器的自感電壓

其中：VMAX = ωLIMAX = √2VRMS，這是最大電壓幅度，θ = + 90°是電壓和電流波形之間的相位差或相位角。即，通過純電感器的電流滯后電壓90度。

在相量域中

在相量域中，線圈兩端的電壓表示為：

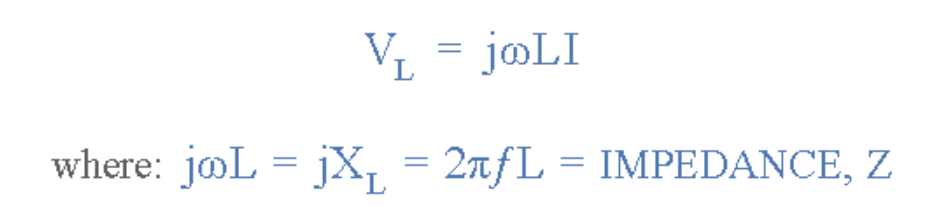
交流電感在相量域中的電壓

在極坐標形式中，這將寫為：XL∠90°，其中：

交流電感阻抗

交流電感

交流電感的阻抗方程

通過串聯R + L電路的交流

我們在上面已經看到，通過純電感線圈的電流滯后電壓90度，當我們說純電感線圈時，我們指的是沒有歐姆電阻，因此沒有I2R損耗的線圈。但在現實世界中，不可能只有純交流電感。

所有電線圈、繼電器、螺線管和變壓器無論使用多少匝線圈，都會有一定的電阻。這是因為銅線具有電阻率。然后我們可以將我們的電感線圈視為一個具有電阻R與電感L串聯的線圈，產生可以松散地稱為“不純電感”的東西。

如果線圈有一些“內部”電阻，那么我們需要將線圈的總阻抗表示為電阻與電感串聯，并且在包含電感L和電阻R的交流電路中，組合兩端的電壓V將是兩個分量電壓VR和VL的相量和。

這意味著通過線圈的電流仍將滯后電壓，但滯后量小于90度，取決于VR和VL的值，即相量和。電壓和電流波形之間的新角度給出了它們的相位差，正如我們所知，這是電路的相位角，用希臘符號Φ表示。

考慮下面的電路，其中純非電感電阻R與純電感L串聯連接。

串聯電阻-電感電路

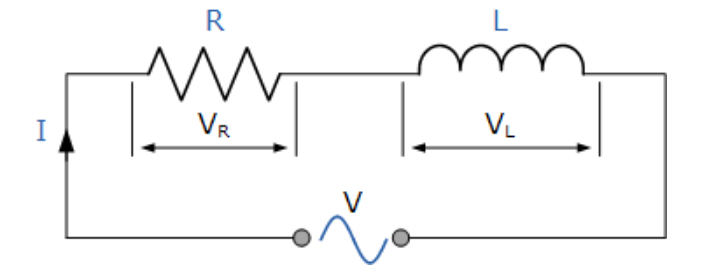
交流電路中的交流電感

在上述RL串聯電路中，我們可以看到電流是電阻和電感的共同部分，而電壓由兩個分量電壓VR和VL組成。這兩個分量的合成電壓可以通過數學計算或繪制矢量圖來找到。

為了能夠繪制矢量圖，必須找到一個參考或共同分量，在串聯交流電路中，電流是參考源，因為相同的電流流過電阻和電感。純電阻和純電感的單獨矢量圖如下：

兩個純分量的矢量圖

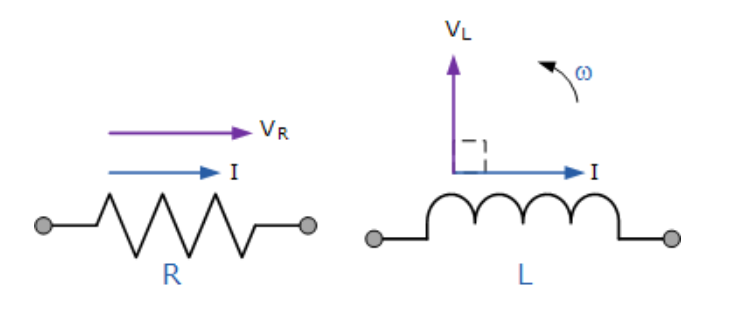
交流電感和電阻的矢量圖

我們可以從上面以及我們之前關于交流電阻的教程中看到，電阻電路中的電壓和電流是同相的，因此矢量VR按比例繪制在電流矢量上。

同樣從上面可知，在交流電感（純）電路中，電流滯后電壓，因此矢量VL繪制在電流前90度，并與VR按相同比例繪制，如圖所示。

合成電壓的矢量圖

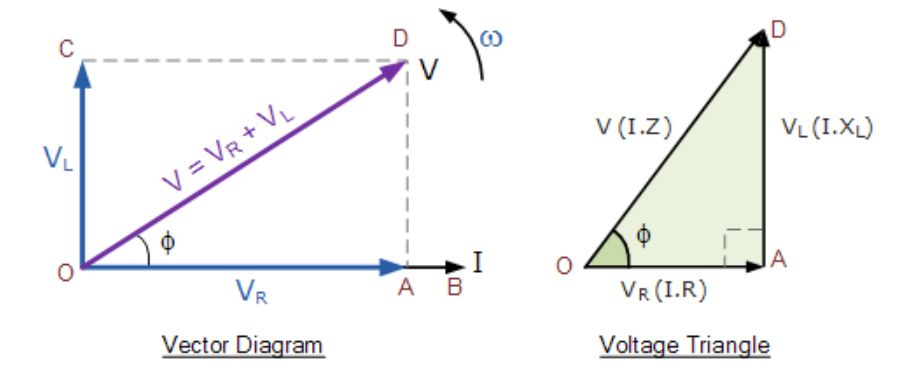
合成矢量圖

從上面的矢量圖中，我們可以看到線°B是水平電流參考，線°A是與電流同相的電阻分量上的電壓。線°C顯示電感電壓，它領先電流90度，因此仍然可以看到電流滯后純電感電壓90度。線°D給出了電源電壓的合成值。然后：

V等于施加電壓的均方根值。

I等于串聯電流的均方根值。

VR等于與電流同相的電阻上的I.R電壓降。

VL等于領先電流90度的電感上的I.XL電壓降。

由于電流在純電感中恰好滯后電壓90度，從單個電壓降VR和VL繪制的合成相量圖表示一個直角電壓三角形，如上圖°AD所示。然后我們還可以使用畢達哥拉斯定理數學地找到電阻/電感（RL）電路上這個合成電壓的值。

由于VR = I.R和VL = I.XL，施加電壓將是兩者的矢量和，如下：

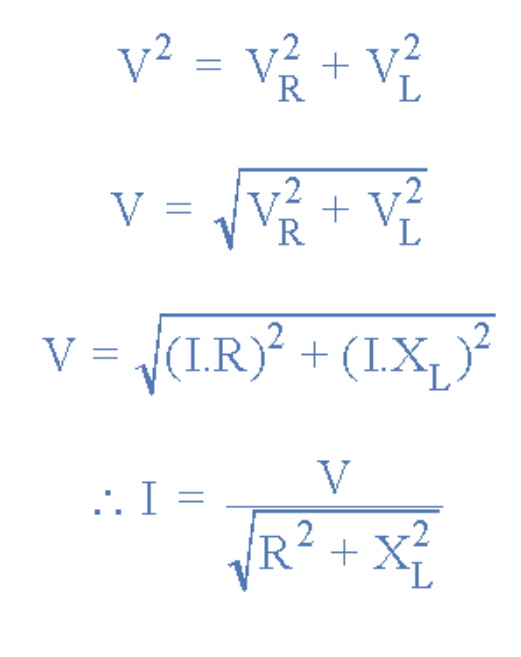
電壓三角形

電路的阻抗量表示電路的阻抗Z。

交流電感的阻抗

阻抗Z是對包含電阻（實部）和電抗（虛部）的交流電路中電流流動的“總”阻礙。阻抗的單位也是歐姆，Ω。阻抗取決于電路的頻率ω，因為這影響電路的電抗分量，在串聯電路中，所有電阻和電抗阻抗相加。

阻抗也可以用復數表示，Z = R + jXL，但它不是相量，它是兩個或多個相量組合在一起的結果。如果我們將上述電壓三角形的邊除以I，將獲得另一個三角形，其邊表示電路的電阻、電抗和阻抗，如下圖所示。

RL阻抗三角形

交流電感的阻抗三角形

然后：（阻抗）2 =（電阻）2 +（j電抗）2，其中j代表90度的相位差。

這意味著電壓和電流之間的正相位角θ如下所示。

相位角

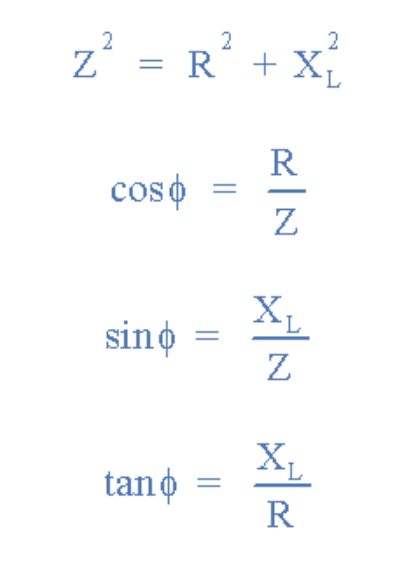
電阻與電抗的相位角

雖然我們上面的例子代表了一個簡單的不純交流電感，但如果兩個或多個電感線圈串聯在一起，或者單個線圈與許多非電感電阻串聯，那么電阻元件的總電阻將等于：R1 + R2 + R3等，給出電路的總電阻值。

同樣，電感元件的總電抗將等于：X1 + X2 + X3等，給出電路的總電抗值。

這樣，包含許多扼流圈、線圈和電阻的電路可以輕松簡化為一個阻抗值Z，它由一個電阻和一個電抗串聯組成，Z2 = R2 + X2。

交流電感示例1

在以下電路中，電源電壓定義為：V(t) = 325 sin( 314t – 30° )，L = 2.2H。確定通過線圈的均方根電流值，并繪制相應的相量圖。

交流電感示例1

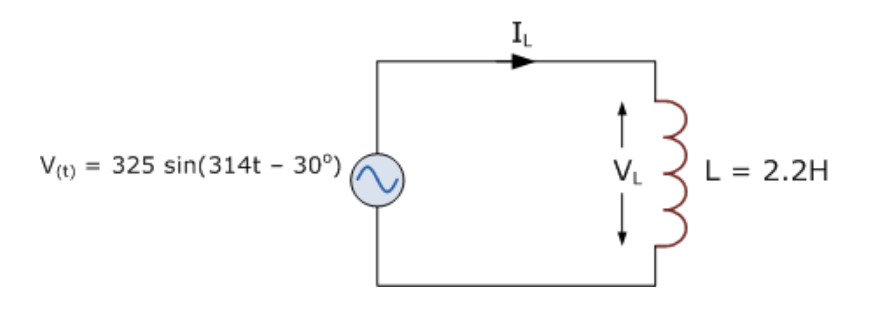
線圈上的均方根電壓將與電源電壓相同。如果電源的峰值電壓為325V，則等效的均方根值為230V。將這個時域值轉換為極坐標形式，我們得到：VL = 230 ∠-30°（伏特）。線圈的感抗為：XL = ωL = 314 x 2.2 = 690Ω。然后，通過線圈的電流可以使用歐姆定律找到：

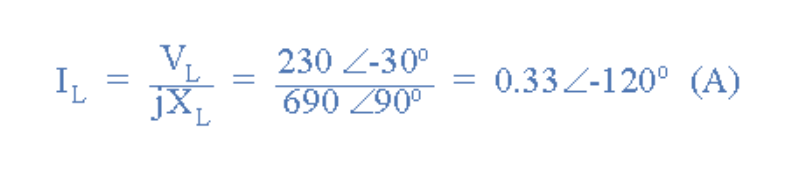
線圈中的電流

由于電流滯后電壓90度，相量圖如下所示。

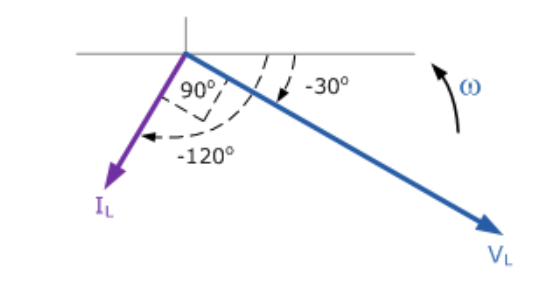
相量圖

交流電感示例2

一個線圈的電阻為30Ω，電感為0.5H。如果通過線圈的電流為4安培。如果頻率為50Hz，電源電壓的均方根值是多少。

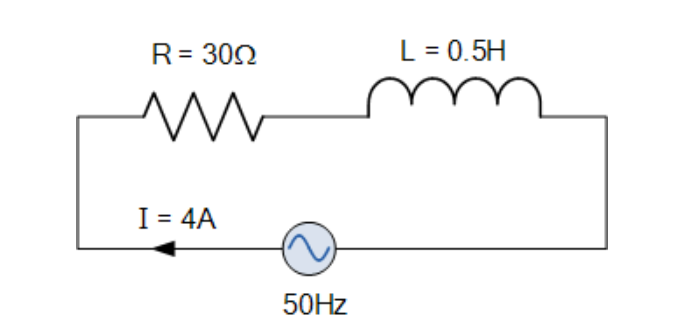
示例2

電路的阻抗為：

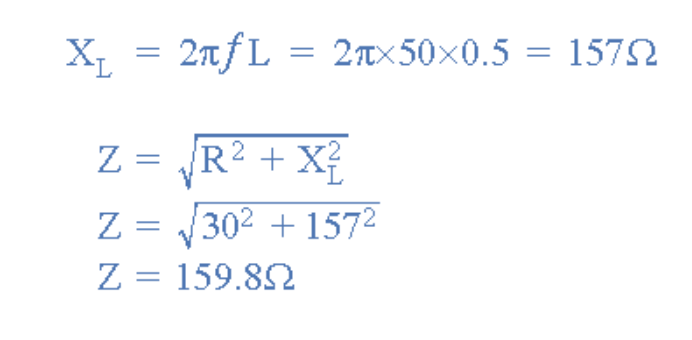
電路阻抗

然后，每個元件上的電壓降計算如下：

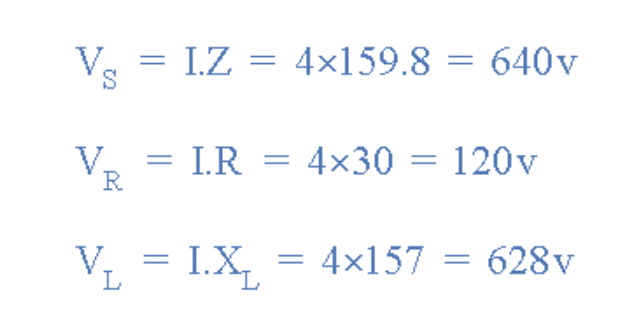
元件電壓

電流和電源電壓之間的相位角計算如下：

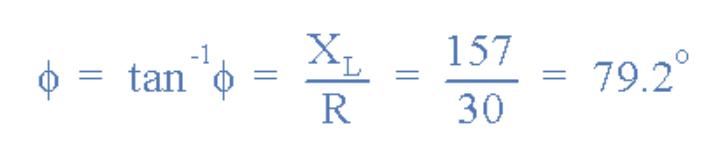
相位角φ

相量圖如下所示。

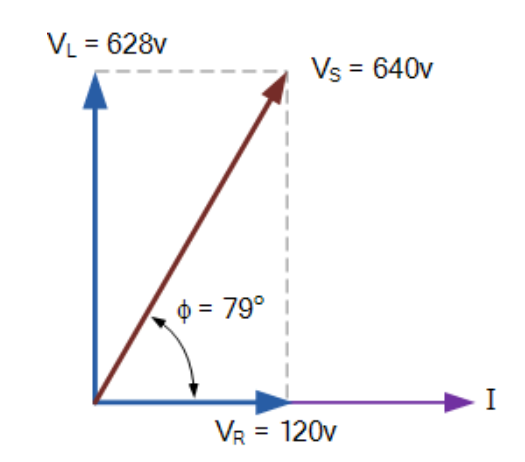
電壓相量圖

在下一個關于交流電容的教程中，我們將研究當穩態正弦交流波形施加到電容器上時，電容器的電壓-電流關系，以及純和非純電容器的相量圖表示。