抖動話題是示波器測量的最高境界，也是最風云變換的一個話題，這是因為抖動是示波器測量的諸多功能中最和“數學”相關的。 玩數學似乎是需要一定境界的。  

1，抖動和波形余輝的關系
有一種比較傳統的測量抖動的方法，就是利用余輝來查看信號邊沿的變化，然后再用光標測量變化的大小（如圖1所示）。后來高端一點的示波器具有“余輝直方圖”的功能，利用余輝直方圖和相關參數可以自動測量出信號邊沿變化的余輝的變化范圍。 在上個世紀90年代初示波器有了真正意義的“測量統計”功能之后，這個方法就逐漸被淘汰了。 

 
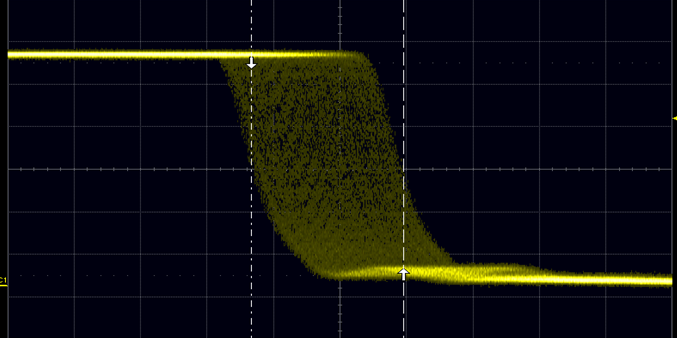
                                    圖1 傳統的抖動測量方法

這種傳統的方法有下面這些缺點：（1）總會引入觸發抖動，因此測量的結果很不準確。（2）只能測量部分參數的抖動，譬如觸發上升沿，測量下降沿的余輝變化，反應了寬度的抖動，觸發上升沿，測量相鄰的上升沿的余輝變化，反應了周期的抖動。顯然還有很多類型的抖動特別是最重要的TIE抖動無法測量出來。 （3）抖動產生的因果關系的信息也無從得知。

2，定義抖動的四個維度
和抖動相關的名詞非常多：時鐘抖動，數據抖動; 周期抖動，TIE抖動，相位抖動，cycle-cycle抖動; 峰峰值抖動(pk-pk jitter)，有效值抖動(rms jitter);總體抖動(Tj)，隨機抖動(Rj)，固有抖動(Dj);周期性抖動，DCD抖動，ISI抖動，數據相關性抖動; 定時抖動，基于誤碼率的抖動; 水平線以上的抖動和水平線以下的抖動…… 這些名詞反應了定義抖動的不同維度。 

    回到“什么是抖動”的定義吧。其實抖動的定義一直沒有統一，這可能也是因為需要表達清楚這個概念的維度比較多的原因。目前引用得比較多的定義是: Jitter is defined as the short-term variations of a digital signal’s significant instants from their ideal positions in time. 就是說抖動是信號在電平轉換時，其邊沿與理想位置之間的偏移量。如圖2所示，紅色的是表示理想信號，實際信號的邊沿和紅色信號邊沿之間的偏差就是抖動。什么是“理想位置”，“理想位置”是怎么得到的？ 這是被問到后最不好回答的問題。 

 
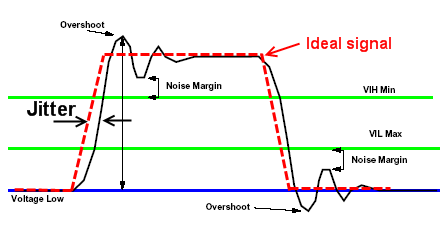
                              圖2抖動的定義

我認為描述抖動離不開“四個維度”。僅僅是說“我想測量抖動”，這是不具體的表達。我建議的一種完整的表達方式是： 我想測量100萬樣本（一定數量樣本）下的時鐘抖動（或 數據抖動）的周期抖動（或 TIE抖動，相位抖動，cycle-cycle抖動）的峰峰值抖動和有效值抖動（或Tj,Rj,Dj）。 具體的測量方法上就是先測量被測信號的周期（或TIE，Cycle-cycle period）等參數，然后持續測量出100萬個甚至更多樣本，將這100萬個樣本下參數測量結果的最大值和最小值相減即為峰峰值抖動。但是10的12次方樣本很難直接測量出來，因為需要消耗的時間太長，所以就改用數學模型預測的方法進行推導。

上面表達中涉及到抖動定義的四個維度是:
（1）測量抖動的樣本數/誤碼率。
（2）被測信號的類型。分為時鐘抖動和數據抖動。 
（3）關注的抖動參數的類型。主要有周期抖動，TIE抖動，cycle-cycle抖動。
（4） 抖動測量結果的類型。主要有峰峰值抖動，有效值抖動，總體抖動（Tj），固有抖動(Dj)，隨機抖動(Rj)。

3，抖動是關于誤碼率的函數
我們下意識里可能會問，被測信號的抖動最壞能有多大？ 其實，隨著觀察到的測量樣本數的增加，這個問題的答案也就不一樣。沒有樣本數的限定，這個問題沒有一個收斂性的答案。抖動是關于誤碼率的函數。誤碼率為10e-12（10的-12次方）即表示發送端發送10e+12（10的12次方）個比特位的信號，在接收端出現誤碼的比特位個數是一個。測量10e-12誤碼率下的抖動可以理解為測量10e+12樣本下的抖動。

4，時鐘抖動VS數據抖動 / 水平線以上的抖動 VS 水平線以下的抖動
當我們在定義抖動具有四個維度時，特別強調被測信號的類型分為時鐘抖動和數據抖動，這是否意味著兩種抖動的測量方法是完全不一樣的呢?   其實，我們可以將時鐘信號理解為一種特別的數據。所有用于數據抖動的測量方法理論上都可以用于測量時鐘，只是因為時鐘信號非常簡單，是規則的010101…碼型，因此，對于時鐘抖動通常是通過直接測量一定數量的樣本（樣本數量應該是多少一般也沒有統一的定義，甚至在有的時鐘芯片手冊中也沒有說明）的參數結果，統計得出參數變化大小的pk-pk值，即為峰峰值抖動（pk-pk jitter）。 峰峰值抖動隨著測量時間的增加，測量結果會變大。峰峰值抖動的測量結果不具備重復性，因為隨機抖動理論上是無限發散的。有效值抖動（rms jitter）表示參數變化大小的標準偏差值。 我們將這種定量方法直接測量出來的抖動形象地稱為“水平線以上的抖動”，因為這種抖動結果是不需要借助數學模型進行推導和預測的。 這種方法的抖動也叫“定時抖動（Timing jitter）”。 時鐘抖動關注的信號參數類型主要有周期(period)，TIE(Time Interval Error)和相鄰周期間（Cycle-Cycle Period），對于時鐘信號的單獨研究，通常三種參數的抖動都需要測量。

數據抖動關注的是一定誤碼率下的TIE抖動，現在的串行數據測量領域通常默認的都是10e-12誤碼率，也就是說需要測量10e+12樣本，這需要示波器測量幾個小時甚至幾天的時間，即使最快的示波器也無法“硬”測量出10e+12樣本的參數來作為測量結果，因此，就需要根據某種數學模型來基于當前一定數量的樣本數測量的結果來“預測”10e+12的樣本下的抖動結果，這種基于數學模型預測的方法測量的抖動叫“水平線以下的抖動”。所謂抖動的風云變幻即在于一直在爭論使用什么樣的數學模型來預測抖動是最準確的。很多抖動相關的文章就是在用一連串的數學公式來說明作者發現的一種新模型是更準確的，看得您云里來霧里去的。

5，認識TIE抖動
為什么TIE抖動是作為測量數據抖動Tj的默認參數呢?  我想里引用參考文獻[1]中的介紹可以幫助我們理解TIE的重要性：

“通信系統的實質是通過一段介質發送或者接收數據。發送端TX發出不同編碼形式的高速串行數據，經過一段鏈路傳輸后到達接收端RX，串行數據在傳輸過程中會受到各種各樣的干擾，引起數據的抖動，串行數據系統工作的目的就是要盡可能的減少這些干擾的影響使得接收端能準確無誤的恢復出發送端發送過來的數據。由于接收端（一般是由D觸發器構成）需要使用時鐘采樣來完成同步接收數據，因此時鐘信號和數據信號之間的同步關系是非常重要的，即必須要滿足一定的建立時間和保持時間。因此串行數據時鐘系統結構的變化最根本上是為了滿足時鐘與數據之間的時序關系，以便接收端能正確的接收到信號。當數據信號的電平發生翻轉后，時鐘邊沿與數據邊沿需要一定的建立時間來鎖存數據；同時，數據信號的電平需要一定的保持時間讓時鐘能穩定的鎖存數據。為了讓建立時間和保持時間最大化，時鐘最好能出現在數據比特位的中央。但是由于數據或者時鐘存在抖動，抖動較大時，無法滿足建立時間和保持時間的要求，D觸發器可能輸出錯誤的數據，產生誤碼。特別是在高速數字電路中，速率的增加導致建立時間和保持時間的余量越來越小，由于抖動產生誤碼的概率越來越高，所以，時鐘和數據的抖動測試非常重要。

研究串行數據系統的抖動主要是研究時鐘與串行數據的相對抖動，而不是單純的指時鐘抖動或者數據抖動。也就是說即使時鐘有很大的抖動，但是只要數據也存在同樣大的抖動，則兩者之間的相對抖動仍舊很小，時鐘和數據之間的建立時間和保持時間也仍舊能夠得到保證。”

如何將時鐘和數據之間的關系聯系起來呢?  TIE（Time Interval Error）！ TIE為作為抖動中最重要的一個參數，我們需要對它有深刻認識。 TIE定義為被測信號邊沿與“參考時鐘”邊沿之間的時間間隔。具體計算中是以和參考電平的交叉點的時刻來計算的，如圖3所示。TIE是在信號和參考時鐘的每一個邊沿都進行測量。                            

 
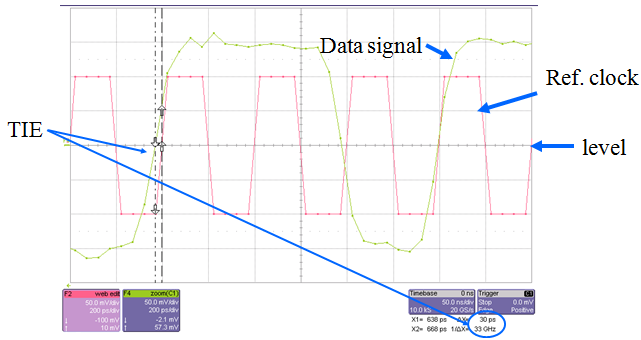
                                         圖3  TIE的定義

產生“參考時鐘”（也就是前面抖動定義中提到的“理想位置”）有幾種方法，比較常用的方法是從被測信號中通過軟件PLL進行恢復。有時侯是直接定義一個理想的參考時鐘，或者是在外部引入一個硬件時鐘作為參考。 PLL的特性是準確測量抖動的關鍵所在，因為產生的參考時鐘的誤差將直接影響到TIE的測量結果，并進而影響到最終的抖動測量結果。關于PLL的具體細節請閱讀參考文獻[2]。
     
6，峰峰值抖動和總體抖動
峰峰值抖動（pk-pk jitter）是水平線以上的抖動，是直接測量出來的。總體抖動（Tj）是水平線以下的抖動，是通過數學模型預測出來的。很多時候當您說要測量Tj時，我就知道您具體要測量什么了，因為這里面有幾個維度是業界的默認設置：Tj通常是指測量10的12次方樣本下的數據抖動的TIE抖動的峰峰值抖動（pk-pk jitter）。前面已述,一般都默認了Tj是基于10e-12的誤碼率的，默認關注的抖動參數是TIE。

7，抖動和眼圖的關系
眼圖在一定程度上反應了抖動的大小，眼圖越“干凈”，眼圖展開程度越大，說明抖動值越小。眼圖的交叉位置在水平軸的區間越小，抖動越小。 在光模塊行業，過去常通過眼圖交叉點位置形成的余輝直方圖來直接測量抖動，余輝直方圖的最左到最右邊的大小范圍即為峰峰值抖動，如圖4所示。在HDMI測量規范中對抖動的定義中也是采用這種方法。按前面所述，這是一種水平線以上的抖動。 交叉點的余輝直方圖呈現高斯分布，說明抖動的行為主要表現為隨機抖動，反之，如果余輝直方圖表現為雙峰分布，說明有明顯的固有抖動。 

 
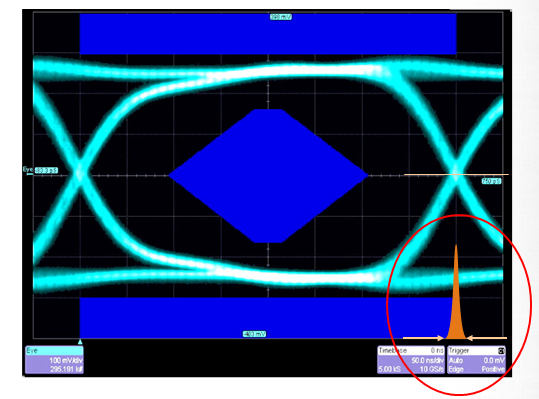
圖4  抖動和眼圖的關系