功率放大器（PA）的輸出功率和效率在很大程度上取決于其負載終端。了解如何通過分析負載線并估計恒定輸出功率的負載牽引輪廓來表征PA的性能。

有源射頻電路的源端和負載端會影響設備性能的重要方面。這就是為什么當我們設計射頻放大器時，我們需要表征有源器件在不同終端阻抗下的性能。在功率放大器（PA）設計中，我們需要特別注意負載阻抗。PA的負載端對它的輸出功率和效率有很大的影響，換句話說，對它的主要性能指標有很大的影響。

對于小信號放大器來說，用S參數來描述器件通常就足夠了，但PA表現出高度的非線性。因此，經典的小信號S參數不能為我們提供對其性能的充分描述。對于PA，我們需要在使用大信號激勵時，針對不同負載阻抗值來表征器件性能。這可以通過一種概念上簡單但非常有效的方法來實現，即負載牽引測量。

什么是負載牽引測量？

負載牽引測量是一種通用技術，其中對受試設備（DUT）呈現的負載阻抗系統地變化。然后記錄每個負載值的性能，并使用該數據獲得感興趣的性能指標的恒定性能輪廓。

使用負載牽引技術，我們可以在阻抗平面上繪制恒定輸出功率和效率的等值線。最好使用史密斯圓圖來完成。圖1顯示了一個典型PA的輸出功率（Pout）和功率附加效率（PAE）的一些負載牽引等值線。

功率放大器的功率附加效率（藍色）和輸出功率（紅色）的負載牽引輪廓。

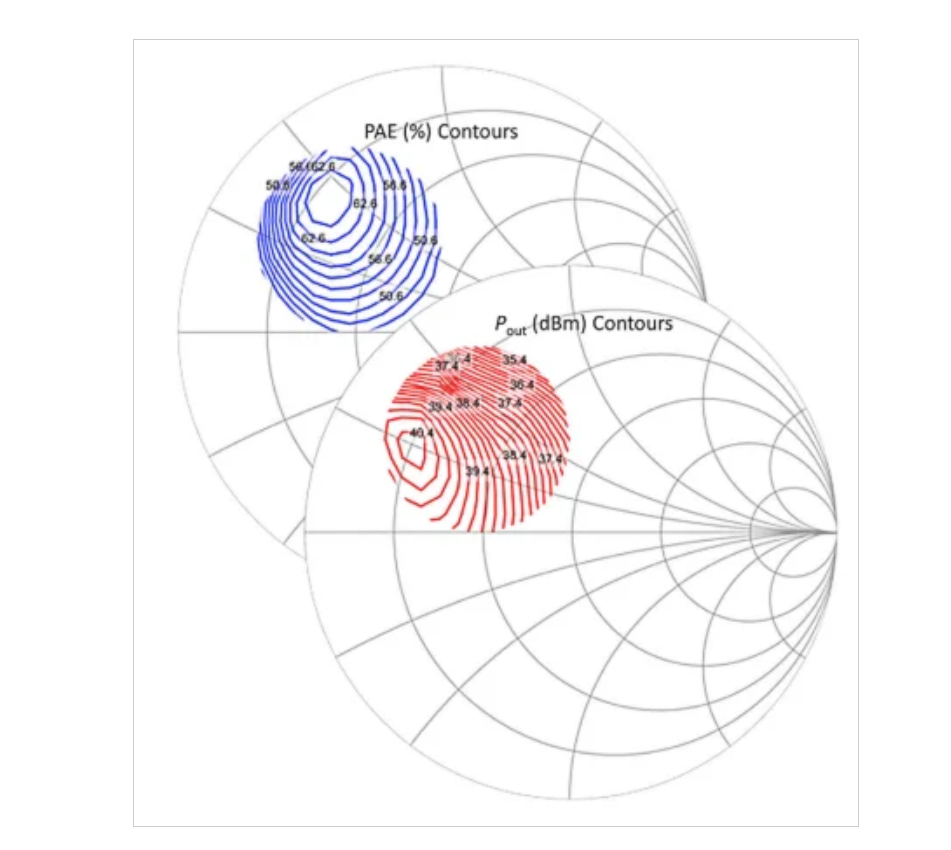
 圖1.PA的功率附加效率（PAE）和輸出功率（Pout）等值線。圖片由羅德與施瓦茨公司提供

負載牽引輪廓使我們能夠考慮器件的非線性響應，并且可以用來設計 PA，就像我們在設計小信號放大器時使用恒定增益或噪聲系數輪廓一樣。它們還可以考慮放大器的封裝寄生效應，盡管這主要超出了本文的范圍。

射頻設計軟件工具通常包括專門用于執行負載牽引測量的仿真工具。這些工具在史密斯圓圖上應用了許多不同的負載阻抗，并對結果進行插值，以構建恒定輸出功率的輪廓。

如果我們有器件輸出和封裝寄生效應的等效電路模型，我們也可以相對容易地估算恒定功率的等值線。在本文的其余部分，我們將看到如何（盡管我們暫時將寄生效應排除在我們的分析之外）。

估算恒定輸出功率輪廓

圖2顯示了圍繞FET器件構建的A類放大器。

A類放大器的電路圖。

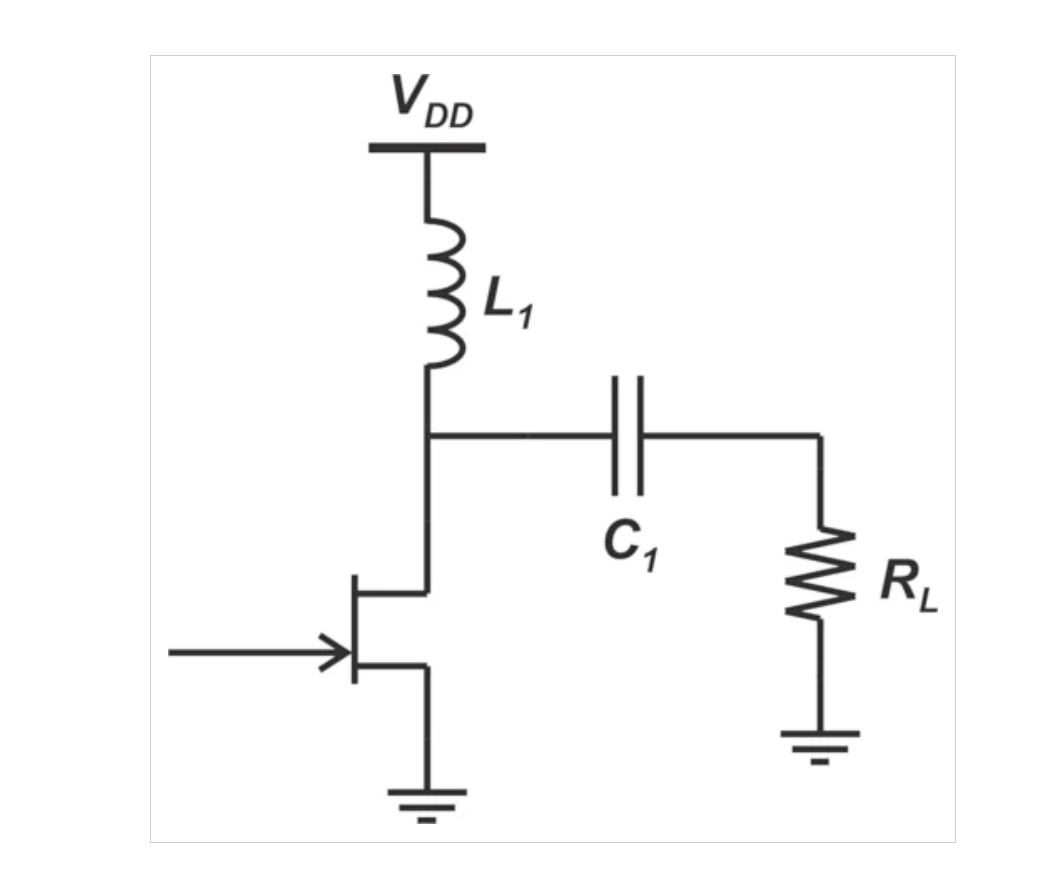
圖2:A類放大器示例。圖片由Steve Arar提供

為了我們的計算，我們將對放大器做出以下假設：

它具有3.5 V電源電壓（VDD = 3.5 V）。

它的最大電流為1A（Imax=1A）。

圖3中的藍色曲線顯示了器件特征曲線的分段線性近似。

特征曲線的膝蓋電壓（vk）遠小于VDD。

最后一個假設對于分析來說并不是嚴格必要的，但它確實使解釋一些相關概念變得更加簡單。

示例功率放大器的特性曲線和最佳負載線圖。

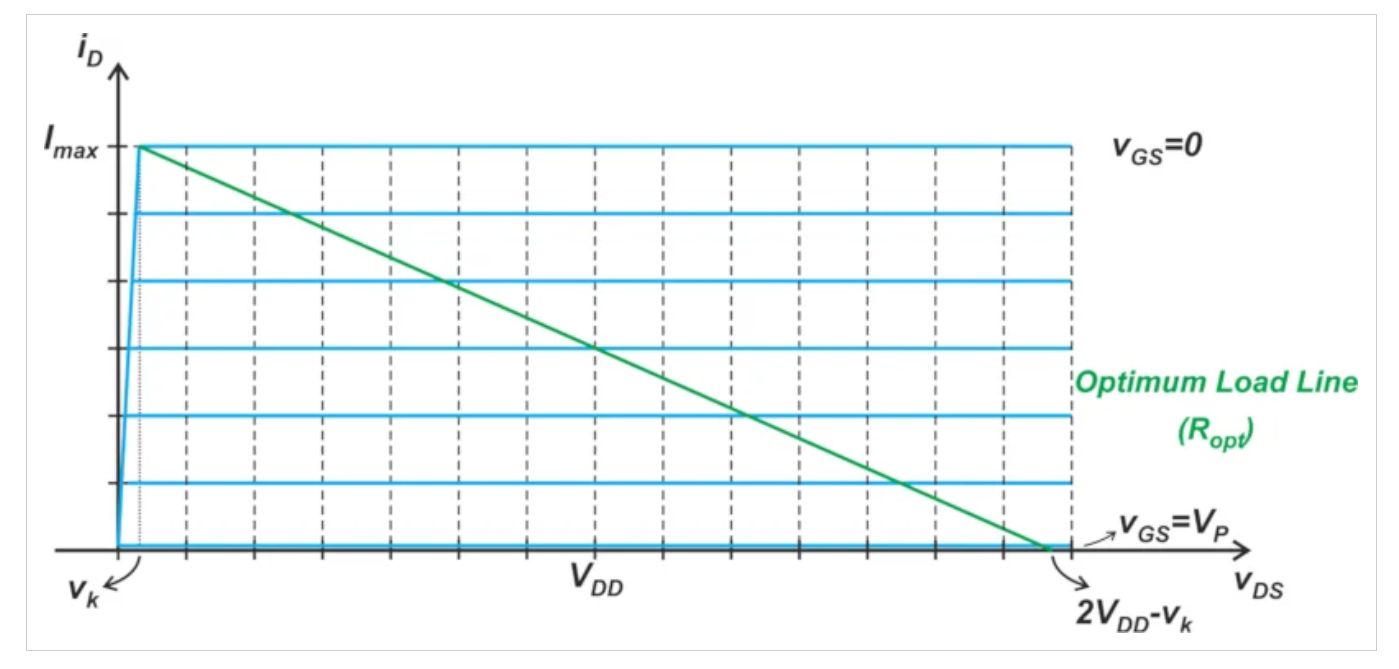
圖3。示例PA的特性曲線（藍色）和最佳負載線（綠色）。圖片由Steve Arar提供

首先，讓我們找到我們的示例放大器的最佳負載和功率。為了實現最大輸出功率，我們選擇適當的負載電阻來偏置負載線中間的晶體管。在vk遠小于VDD的情況下，最佳偏置點為VDSQ=3.5V和IDQ=0.5A。我們使用偏置點和圖3中的信息來找到最佳負載電阻：

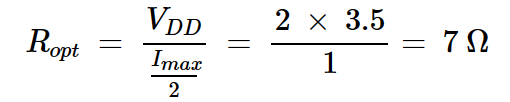
方程式1

最大輸出功率：

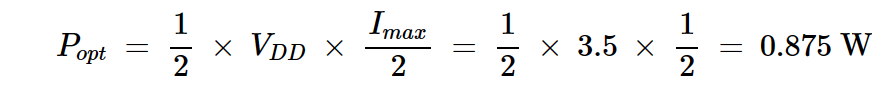
方程式2

該功率放大器的最佳輸出功率為Popt = 0.875 W，實現最佳負載電阻為Ropt = 7 Ω。

現在我們有了必要的信息，讓我們找到這個放大器的負載終端，它產生的輸出功率為0.375W。

通過降低RL來降低輸出功率

我們的目標是找到一個負載電阻，將輸出功率從0.875 W降低到0.375 W。很明顯，我們可以通過降低輸出電阻來降低輸出功率——圖4中的紫色線顯示了當我們這樣做時負載線是如何變化的。

最佳負載電阻和新的較小負載電阻的負載線圖。

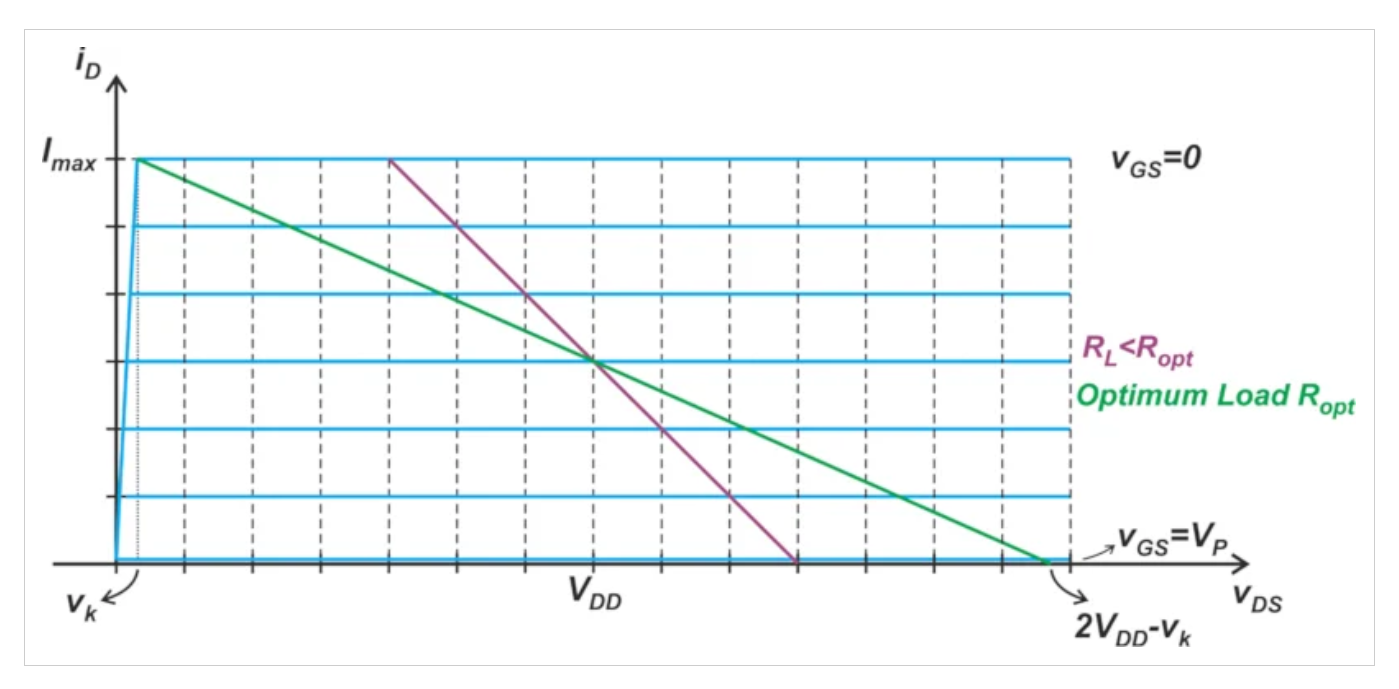
圖4. Ropt（綠色）和新的較小負載電阻（紫色）的負載線。圖片由Steve Arar提供

我們仍然具有最大可能的電流擺動，但電壓擺動已經減小。由于現在的電流擺動仍然等于最佳負載的電流擺動，因此通過以電流表示輸出功率，我們可以更容易地與Popt進行比較：

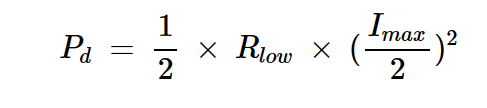
方程式3

其中Rlow是產生較小輸出功率的新負載。

方程式2也可以根據最大電流擺動進行重寫：

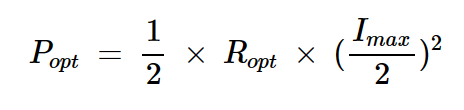
方程式4

用方程式3除以方程式4，我們得到：

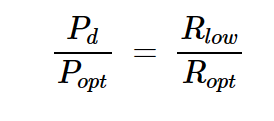
方程式5

將Popt = 0.875 W、Pd = 0.375 W和Ropt = 7Ω代入，我們得到Rlow = 3Ω。圖4中的紫色負載線證實了這一點——它的斜率為-1/3，這意味著它對應于3Ω的負載電阻。

正如負載線清楚地表明的那樣，較小的電阻通過降低電壓擺動來降低輸出功率。如果我們使用大于Ropt的電阻，我們也可以通過相反的方法來實現更小的輸出功率——保持電壓擺動在其最大值并減小電流擺動。讓我們試試吧。

通過增加RL降低輸出功率

圖5中的橙色線顯示了當我們增加負載電阻時負載線是如何變化的。

三條不同負荷線的圖形，其中一條高于最佳負荷線。

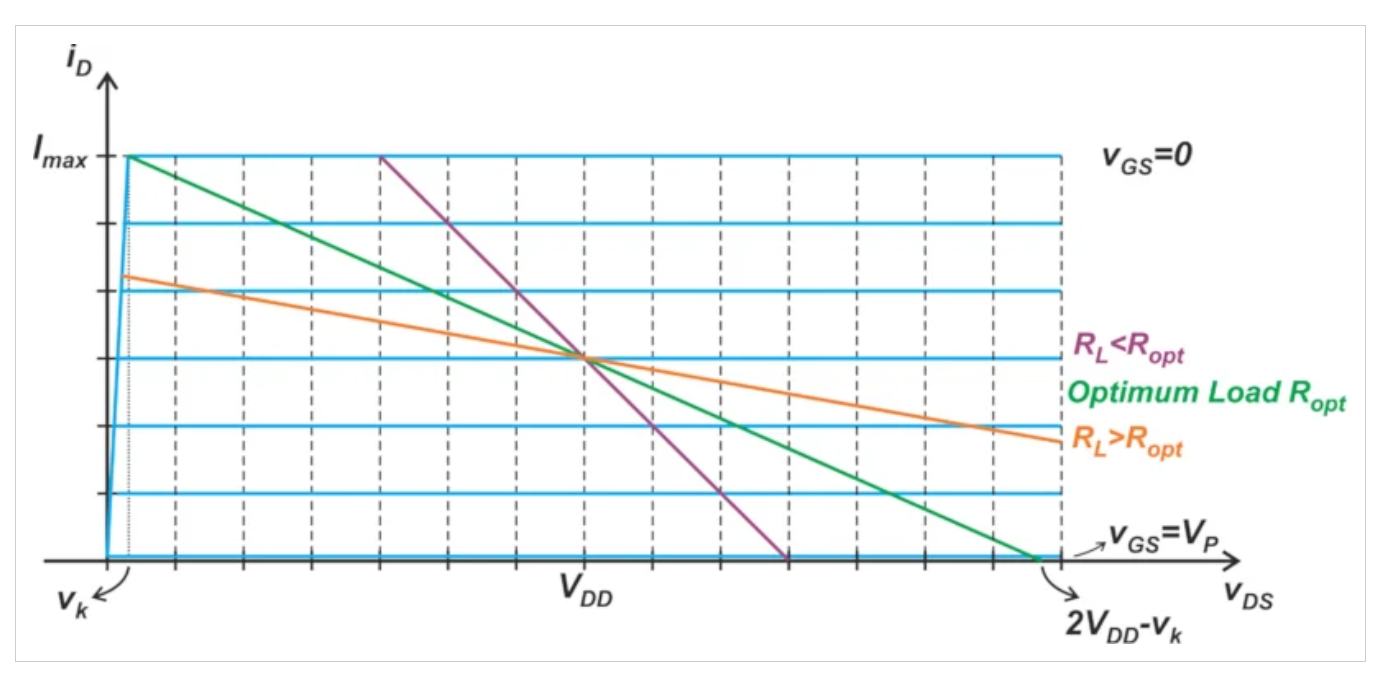
圖5.示例A類放大器的負載線。Ropt為綠色，RL < Ropt為紫色，RL > Ropt為橙色。圖片由Steve Arar提供

電路仍然具有最大電壓擺動。但是，與最佳負載相比，它的電流擺動較小。由于電壓擺動等于最佳負載的電壓擺動，我們可以根據電壓寫出輸出功率，以便更容易與Popt進行比較：

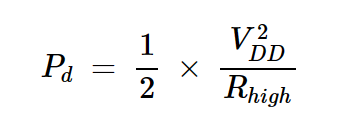
方程式6

其中Rhigh是新的更高的負載電阻，它降低了輸出功率。

我們還可以根據電壓擺動重寫Popt（方程式2）：

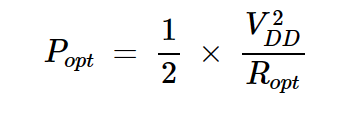
方程式7

方程式6和7得出：

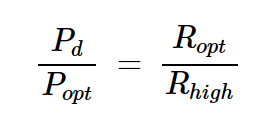
方程式8

Popt = 0.875 W，Pd = 0.375 W，Ropt = 7 Ω，我們得到Rhigh = 16.33 Ω。圖5中橙色負載線的斜率大約等于?1/16.33，對應負載電阻Rhigh=16.33Ω。

為了在史密斯圓圖（圖6）上表示我們的結果，我們將Rlow和Rhigh歸一化為50Ω。這產生了歸一化值0.06和0.33（3/50和16.33/50），分別。

史密斯圓圖顯示了我們之前發現的兩個新負載電阻的歸一化值。

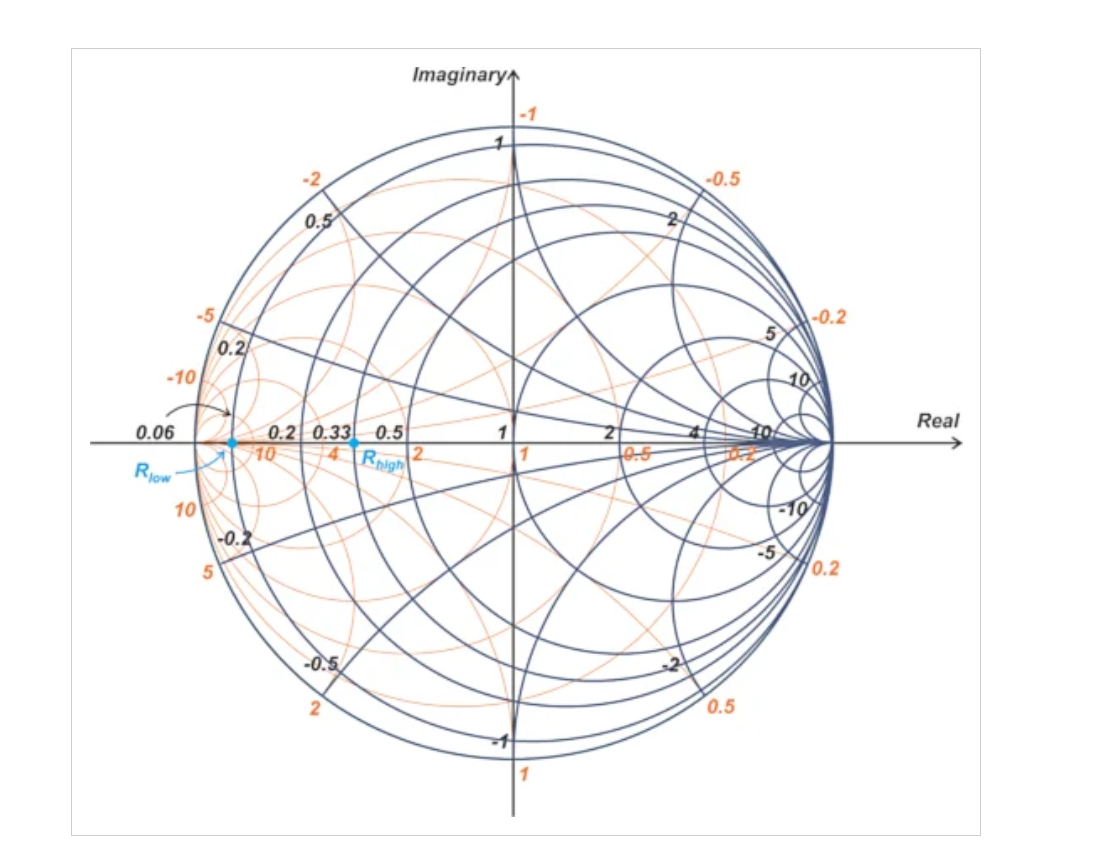
圖6.史密斯圓圖顯示了Rlow和Rhigh的歸一化值（均以藍色標記）。圖片由Steve Arar提供

總結一下我們迄今為止學到的內容：如果最大輸出功率為Popt，我們可以應用方程5和8來找到兩個不同的電阻負載（Rlow和Rhigh），產生輸出功率Pd。但是，如果我們使用復雜的終端而不是純電阻負載，會發生什么？讓我們來找出答案。

添加響應式組件

假設我們的負載終端（ZL）是Rlow加上一些電抗：

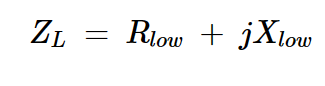
方程式9

傳輸到負載的平均功率仍然由方程2給出。然而，增加的電抗會影響負載兩端的電壓。當RL<Ropt時，最大峰峰電流擺幅為Imax，因此ZL的復阻抗的最大峰峰電壓擺幅為：

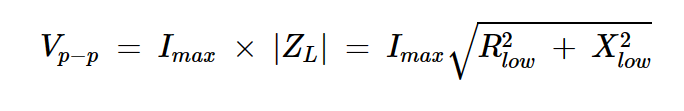
方程式10

從我們上面的負載線分析中，我們知道負載上的峰峰電壓小于或等于2VDD。因此，我們有：

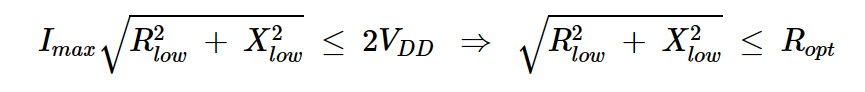
方程式11

其中，方程式1用于獲得以Ropt為變量的最終表達式。我們可以將上述表達式簡化為：

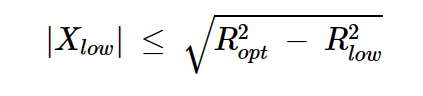
方程式12

該方程式確定了在不違反最大電壓擺動約束的情況下，Rlow可以增加多少電抗。

代入Ropt = 7 Ω和Rlow = 3 Ω，我們觀察到|Xlow|必須小于或等于6.32 Ω，對應于歸一化值0.13。圖7中的藍色曲線顯示了歸一化實部為0.06的阻抗，|Xlow| ≤ 0.13。

史密斯圓圖顯示了通過向Rlow添加電抗而獲得的最終輸出功率輪廓的一部分。

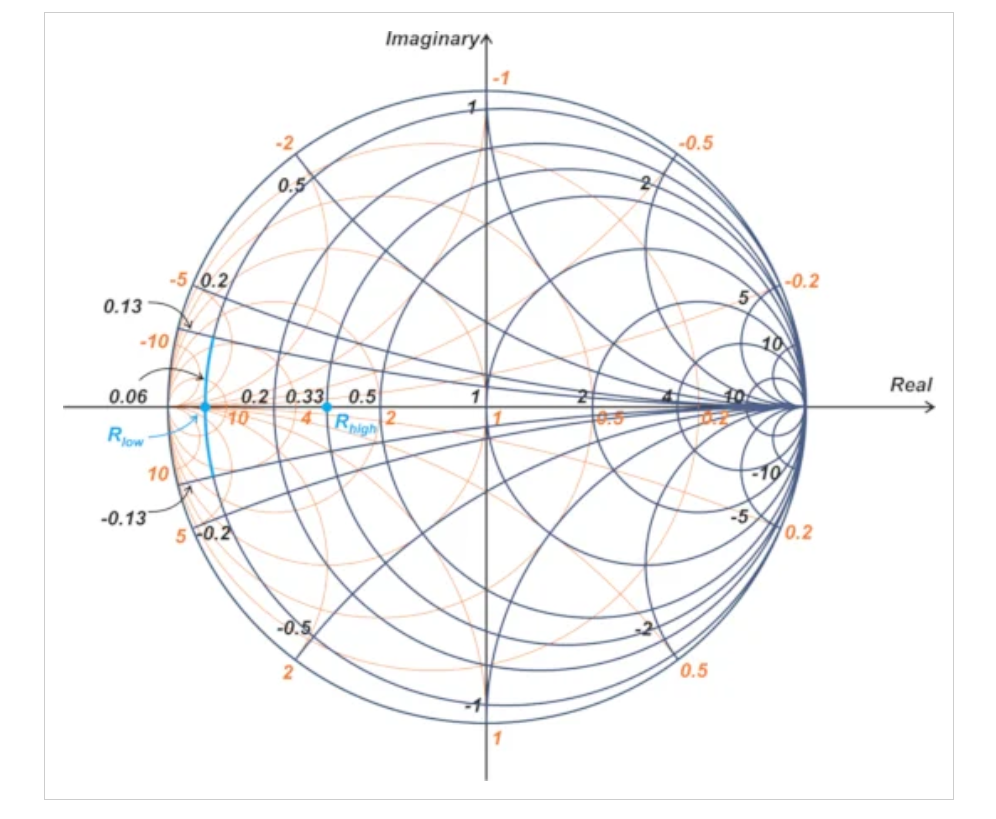
圖7.史密斯圓圖顯示了將電抗添加到Rlow后最終輸出功率輪廓的部分。圖片由Steve Arar提供

現在我們已經為Rlow添加了一個反應性組件，讓我們考慮對Rhigh做同樣的事情。當RL>Ropt時，負載上的最大峰間電壓擺動是恒定的（約2VDD）。因此，我們可以將負載描述為導納而不是阻抗，從而簡化我們的方程。

假設負載導納為：

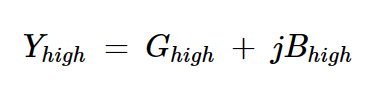
方程式13

其中Ghigh是Rhigh的倒數。將電納Bhigh添加到負載終端不會改變耗散的平均功率；方程6仍然給出了傳遞給負載的平均功率。然而，添加的電納會影響流經負載的電流。

由于最大峰峰電壓擺動等于2VDD，我們可以使用以下等式來計算峰峰負載電流：

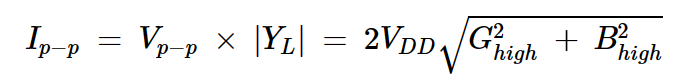
方程式14

根據我們的負載線分析，我們知道通過負載的峰峰電流小于或等于Imax。因此，我們有：

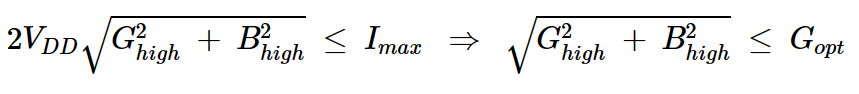
方程式15

方程式1用于根據Gopt寫出上述方程式，Gopt是Ropt的倒數。我們可以將這個方程式進一步簡化為：

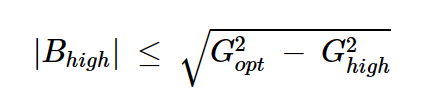
方程式16

在我們的例子中，Ropt = 7 Ω，Rhigh = 16.33 Ω，這導致|Bhigh| ≤ 0.13 S。這對應于史密斯圓圖上的歸一化值0.13×50=6.5。下面，圖8顯示了我們所需的0.375 W的最終恒定輸出功率輪廓。

史密斯圓圖顯示了我們的示例PA的0.375 W恒定輸出功率輪廓。

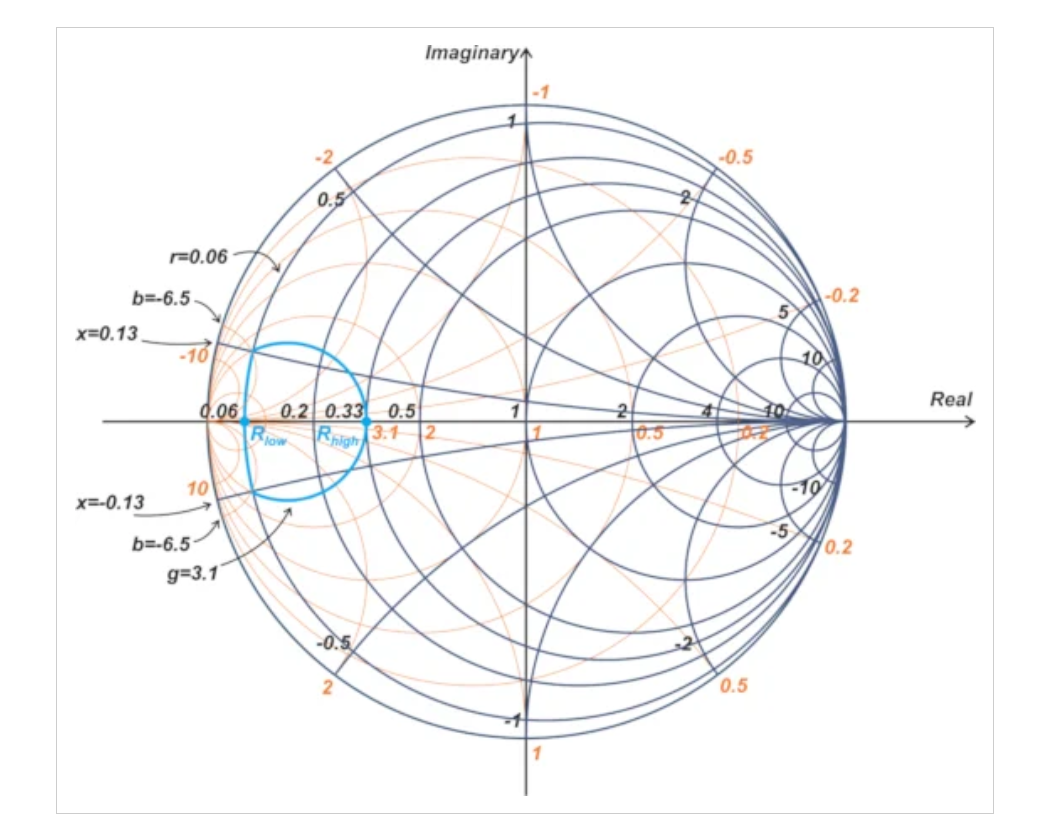
圖8.我們示例PA的0.375 W恒定輸出功率輪廓。圖片由Steve Arar提供

請注意，向Ghigh添加電納相當于沿著穿過Ghigh的恒定電導圓移動。

最終輪廓包括：

恒定電阻圓的一部分，穿過Rlow。

圓的一部分，穿過 Rhigh。

在上面的圖中，這兩個圓分別表示為r = 0.06和g = 3.1。輪廓從電阻性負載延伸到r = 0.06和g = 3.1圓相交的點。這不是巧合，對于任意期望的輸出功率值都會發生這種情況。

這一觀察大大簡化了尋找恒定功率輪廓的過程——我們只需要使用方程 5 和 8 找到輪廓的電阻點（Rlow 和 Rhigh）。然后，我們找到穿過 Rlow 的恒定電阻圓和穿過 Rhigh 的恒定電導圓的交點。

恒定功率等值線從電阻性負載延伸到兩個交點。在這些交點處，同時達到方程11和15規定的最大電壓和電流限制。

圖9顯示了上述示例的另外兩個恒定功率輪廓。綠色輪廓對應于0.236 W或23.74 dBm的功率水平；紫色曲線對應于0.594 W或27.74 dBm。

我們示例功率放大器的三個恒定輸出功率輪廓。

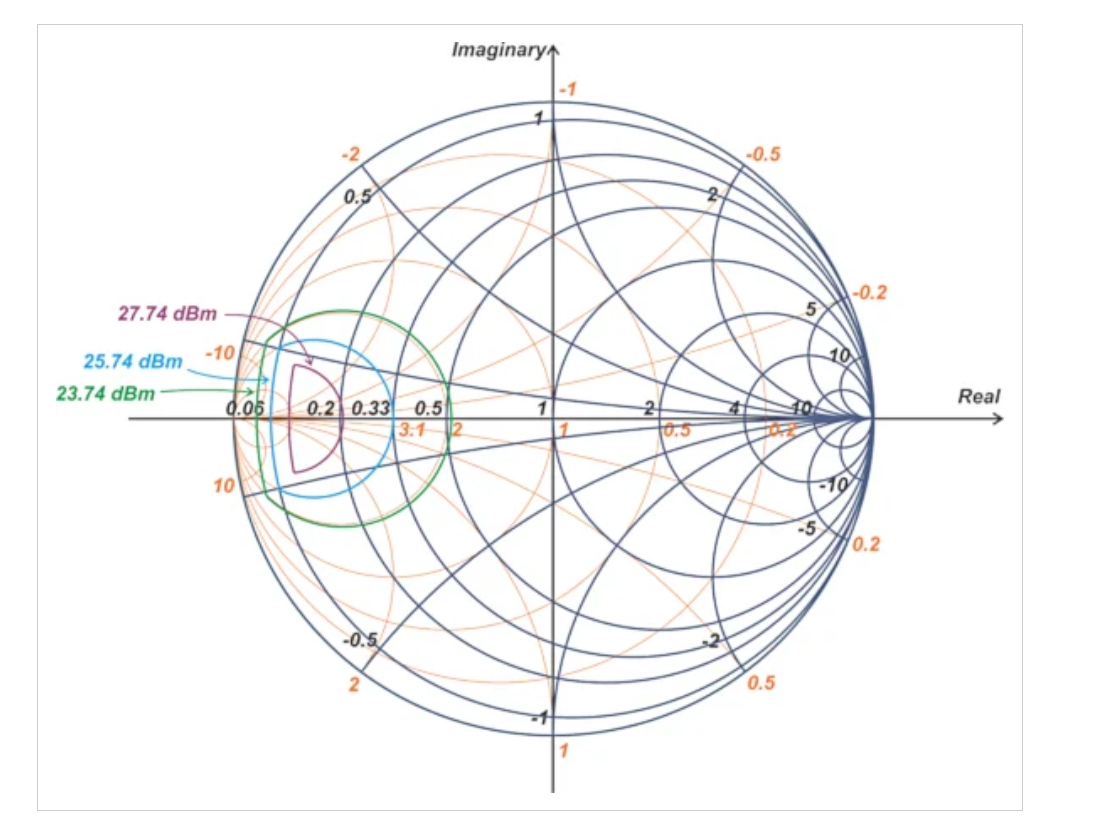
圖9.示例PA的三個恒定輸出功率輪廓，標記為綠色、藍色和紫色。圖片由Steve Arar提供

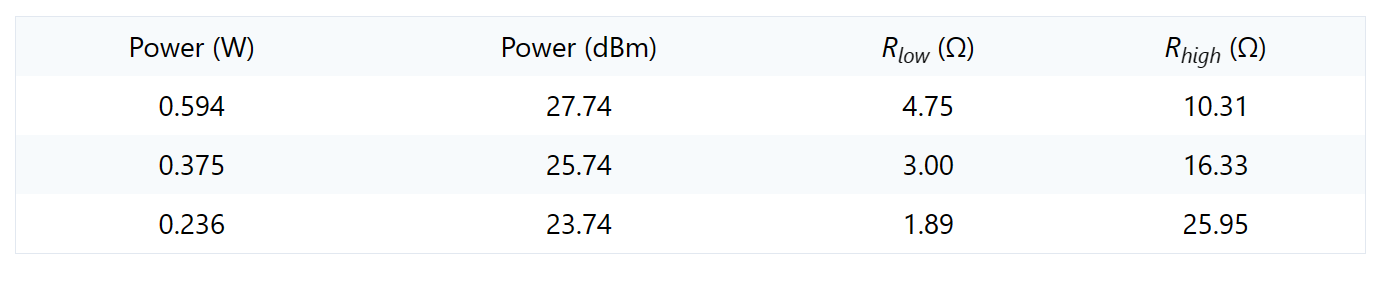
表1列出了每條恒定功率曲線的電阻負載。

表1. 圖9中恒定功率曲線的電阻負載。

考慮器件寄生效應

我們獲得的等值線決定了將連接到晶體管內部電流源的負載終端。然而，我們的分析忽略了寄生元件，包括晶體管的漏源電容和封裝的寄生電容和電感。如果我們考慮寄生效應，我們獲得的等值線將映射到史密斯圓圖上的新等值線。最終結果將類似于圖1中的紅色曲線。