1   研究背景

輪軌間的黏著力其大小因黏著系數而不同，當機車的輪周牽引力或制動機施加的力超過輪軌間所能產生的黏著力最大值時，會造成黏著破壞，機車動輪就會發生空轉或滑行等影響行車安全的現象，影響機車車輛的牽引性能和制動性能，使加速或制動列車所需要的距離增加，除了影響機車運轉安全性及能量浪費外，還會造成軌道或車輪的磨損，使維修成本大大提高，旅客舒適度也會受影響^[1]。解決這類問題最主要的方法是改善輪軌間的黏著條件。試驗顯示，如果輪軌界面有水、油或其他介質，黏著系數會顯著下降^[2]。而采取撒砂裝置噴灑增粘劑可以明顯改善輪軌狀況，提高黏著系數^[3]。

圖1 電力機車撒砂裝置實物圖

現階段列車撒砂系統對撒砂操作的判斷多由駕駛員人工決定是否撒砂和撒砂量的多少。這種人為干預下的撒砂邏輯判斷會造成以下問題:

1. 撒砂滯后，機車在行駛途中，當遇到突發情況需要剎車，此時列車因為制動輪軌間需要的黏著力急劇改變而需要進行撒砂操作，而司機因為無法提前預知緊急情況的發生，無法提前做出撒砂判斷。會嚴重影響列車的行駛安全。

2. 撒砂量過多或過少，撒砂對改善輪軌間黏著有顯著作用。而撒砂量的多少直接影響著增黏效果，撒砂量太少起不到增黏效果。撒砂量太多會造成對輪對的損壞、粉塵污染、影響信號系統使用等一系列問題。因此應在滿足輪軌間黏著力的要求下盡可能少的撒砂。

為了解決以上問題，優化電力機車撒砂功能。文小春等人提出基于模糊控制的機車智能撒砂控制方法，綜合考慮機車加速度、速度、蠕滑速度。建立以機車加速度、機車速度和機車蠕滑速度為輸入，撒砂動作信號作為輸出的控制系統。在控制方法上根據系統特點采用模糊控制方法。最終根據系統的輸出信號來驅動撒砂裝置閥門實現機車撒砂裝置自動撒砂^[4]。王飛寬等人引入一種AHP層次分析法，將機車運行時的速度、加速度、蠕滑速度、級位作為判斷機車撒砂裝置是否撒砂的評價因素。提高撒砂裝置的智能化程度，使機車運行更加安全可靠^[5]。但是此類方法只將問題聚焦于撒砂裝置是否撒砂而不考慮撒砂裝置在不同運行情況下撒砂量的問題。仍然存在機車撒砂裝置撒砂量過多或者過少的問題。為了解決這一問題，在已有的針對電力機車撒砂控制研究基礎上，運用層次分析法獲得列車運行時所需的最佳撒砂量。運行神經網絡對數據訓練，簡化運算過程方便計算。

2 層次分析法

2.1 建立層次結構模型

機車的撒砂量受到多種因素影響，針對這一特點，對機車撒砂量的決策判斷可運用層次分析法來實現。層次分析法（AHP 算法）適用于對難以定量描述的系統做出決策，在對復雜系統的分析上具有重要意義。

AHP算法把各影響因素分成不同層次，使需解決的問題轉化為層次結構模型中，最低層相對于最高層的相對重要權值的確定。計算時對同層次的不同因素，分別按照上層的一個因素為準則進行兩兩比較，以計算出各層因素之間的權重值，并以組合權重值來做出確定最終決策^[6]。

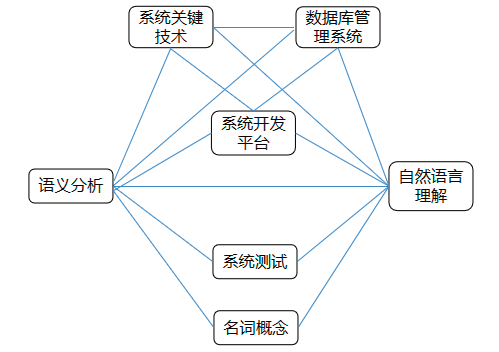
針對列車撒砂系統，對影響機車車撒砂系統的因素從實際工程經驗和各類文獻出發可得出如下結論。當機車運行于級位后半段時，對牽引力的需求更大，因此對撒砂的期望更大。當機車速度較低時，車輛處于加速或減速狀態，此時對撒砂的期望更大。當速度增大后，機車處于平穩運行狀態，對撒砂期望減小。機車加速度一定程度反應機車運行狀態，當加速度比較大時，機車一般處于加速啟動或減速制動狀態，此時對撒砂的期望越大。相反當加速度比較小時，機車處于平穩運行狀態，撒砂期望減小。機車蠕滑速度代表機車輪緣速度相對于機車輪對速度的差值，是空轉滑行程度的指標。蠕滑速度越大越傾向于撒沙^[7]。因此以上述選定因素為準則建立如下層次結構模型：

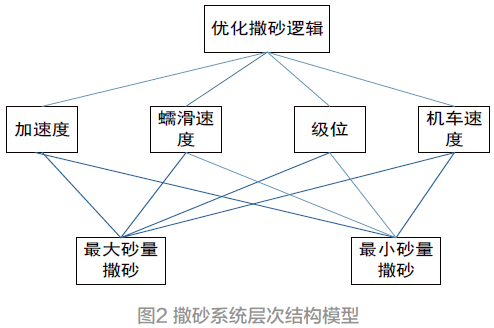
2.2 構建成對比較矩陣

根據圖1所示層次結構模型，當在確定各層次各因素之間的權重時，為盡可能減少性質不同的因素相互比較的困難，提高精準度。Saaty等人提出一致矩陣法，通過對影響因素進行兩兩相互比較，而不是把所有因素放在一起比較，并對比較結果使用相對尺度的方法。對于某一準則，將其下的各方案進行兩兩對比，并根據其重要性的程度評定等級。將兩兩比較結果以矩陣形式表示，此矩陣稱為成對比較矩陣。成對比較矩陣是表示本層所有因素針對上一層某一個因素( 準則或目標) 的相對重要性的比較結果。比較矩陣的元素aij 表示的是第I個元素相對于第J 個元素的比較結果，其中：

其比較結果采用Satty提出的9標度法確立，見表1。

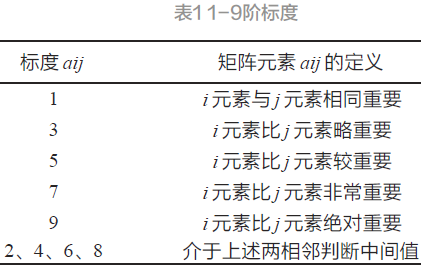
2.2 準則層到目標層的比較矩陣

根據列車運行中對撒砂量要求的實際情況與文獻中多個專家經驗評估認為機車加速度不能反映整車牽引力的需求，當機車加速度過大時，噴射到軌道上的增黏砂會對輪對踏面造成損壞。并且加速度較大的時候，砂粒在踏面和軌道之間摩擦會損傷踏面，此時列車對撒砂量的要求應該盡可能小，所以輪緣加速度對撒沙問題影響因素取為基準值。根據基準值由專家對各影響因素按照1-9標度打分評估。構建比較矩陣圖2。

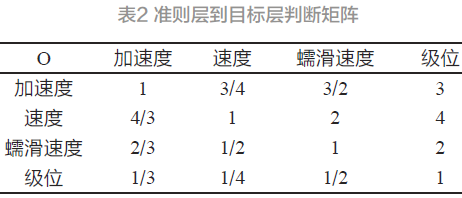
2.3 層次單排序及一致性檢驗

將表二以矩陣形式表示如下：

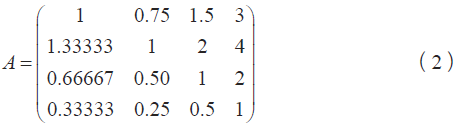
層次單排序前，需要驗證成對比較矩陣是否合理。即要對成對比較矩陣進行一致性檢驗。確定矩陣的不一致范圍是否在一定的誤差下。假設矩陣A 中任一元素都滿足式一，即稱該矩陣為一致性矩陣，一致性矩陣具有以下性質：

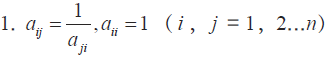
2.A^T也是一致矩陣對應

3.A^T的各行成比例，且各列也成比例

4.A的最大特征值為λ=n，其余的n?1個特征根都為0

5. A的任一列( 行) 都是對應于特征根n 的特征向量。

2.4 方案層到準則層的比較矩陣

要確立最佳撒砂量，需要將準則層各個因素對方案層撒砂量的影響轉換為比較矩陣。準則層對方案層的影響程度可以使用權重函數來定義。定義函數F(x)，結合參考文獻與實際情況可定義如下四組權重函數：

（1）加速度權重函數

當機車處于啟動或制動狀態時，加速度最大。此時對撒砂的需求也更大，因此可定義如下加速度函數。

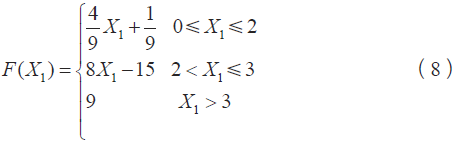
（2）速度權重函數

機車處于啟動狀態時，速度較小。對牽引力的發揮有更高要求，此時對撒砂量的要求也更大，隨著速度的增加，撒砂需求減少。當增長到持續速度附近時，以機車的持續速度為臨界條件。各機車的持續速度會有差異，本文中選取45 km/h 為持續速度

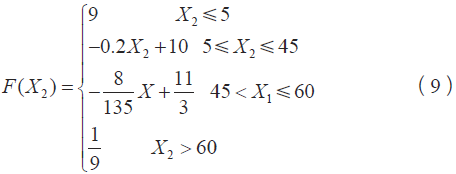
（3）蠕滑速度權重函數

機車蠕化速度能夠衡量車輛空轉或滑行的程度，蠕化速度越大，機車空轉/ 滑行越嚴重。對撒砂量需求更大。

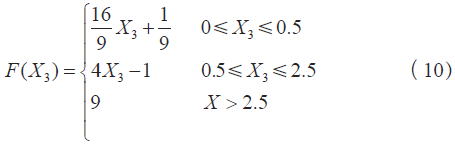
（4）機車級位權重函數

大級位條件下，機車對牽引力有更大的需求，對撒砂量的要求也更大。

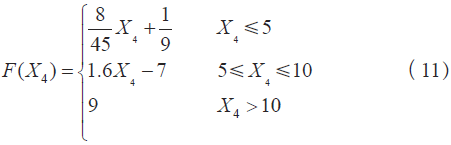
根據權重函數可以得出方案層到準則層的四組成對比較矩陣A₁、A₂、A₃、A₄. 其中

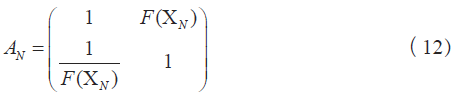
2.5 層次總排序及其一致性校驗

分別計算完下一層對上一層的層次單排序后，從最高層開始，依次計算某一層次的所有因素對于最高層相對重要性的權重值。圖一撒砂系統層次結構模型圖從上到下依次為目標層、準則層、決策層。分別定義為O層（目標層），A 層（準則層），B 層（決策層）準則層4個準則元素加速度、速度、蠕滑速度、級位分別為A₁，A₂， A₃， A₄。根據式(6)可得出A層4個元素對總目標的排序：

根據式（10）的比較矩陣可求出B層元素對A層元素的層次單排序為：

W_B的取值根據權重函數的取值不同。分別計算出A層、B層的層次單排序后。再計算B層的層次總排序，此時有：

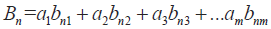
即B層第i個元素對總目標的權值為：

與層次單排序一致，層次總排序也需要進行一致性檢驗驗證矩陣矩陣的取值是否合理。設B層B₁、B₂、B₃、B₄、B5對上層A 層中因素A_j（ j =1, 2,3...m ）的層次單排序一致性指標為CI_J ，隨機一致性指標為RI_j 則可求出層次總排序的一致性比率為：

當CR<0.1 時，則可認為層次總排序滿足一致性條件。

3   案例分析

對運行中的機車假定一組運行條件。假設機車參數加速度2.2 km/h、速度40 km/h、蠕滑速度1 km/h、級位選擇6 檔。

3.1 準則層到目標層層次排序

此時首先根據層次結構模型圖一算出準則層到目標層的一組權重向量，即為式(7)的向量W_A。根據判斷矩陣A[式(2)]和式(6) 按照幾何平均法可求出準則層到方案層的權重向量W_A：

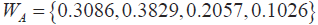
此權向量中有4個元素，每一個元素代表的是同一層次因素對上一層的因素的排序權重。針對此權重向量W₁，代表的含義就是加速度、速度、蠕滑速度、級位對于影響優化撒砂量的重要性。根據式求出成對矩陣的最大特征值：λ_max=4.000 075 ，根據式和式可求出一致性比率CR=0.0187 ，小于0.1。矩陣通過一致性檢驗，W₁可為準則層到目標層的權重向量。

3.2 方案層到準則層層次排序

加速度為2.2 km/h。根據加速度權重函數可定義加速度的判斷矩陣如下：

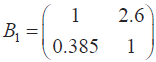
根據式(6)可求出方案層到準則加速度的權重向量：

根據式可求出該矩陣最大特征值 λ_b1 = 2.000 5， 因為該判斷矩陣為二階矩陣，可以認為具有完全 一致性。因此不需要進行一致性檢驗。同理，可 得出其他因素的權重向量如下：

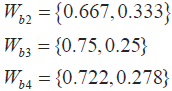
3.3 層次總排序

已知準則層到目標層單排序：

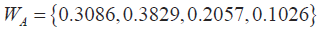
方案層到目標層單排序：

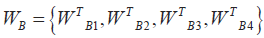
根據式可求出最終的層次排序為

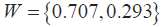
4   方法應用

根據層次分析法算出的結果為0-1的一組數字，代表的是撒砂的趨勢，例如輸出為0.8代表撒砂意向強烈，而輸出為0.4時代表撒砂意向不強烈，系統傾向于少量撒砂甚至不撒砂，并不是實際撒砂量。根據實際工程經驗，撒砂量的確立并不要求十分準確，只需要在一定的范圍內即可。因此可以考慮根據層次分析法得出的結果設置不同擋位，分別對應不同撒砂量。以此優化撒砂邏輯，避免多撒或者少撒砂情況的出現。

層次分析法的計算過程較為復雜。且機車運行時運行狀況會不斷改變，此時根據層次分析法計算出的結果也會不斷改變。為了簡便計算，通過假定多組初始數據（即機車加速度、速度、蠕滑速度、級位）來得到一組數據集，將得到的數據集用神經網絡進行訓練。訓練后的神經網絡只需要設定初始輸入值就可以得出最終結果，省去了大量的計算過程，方便了在線計算^[9]。

以四十組數據為例，將數據進行訓練后得到下圖

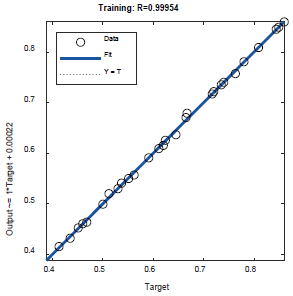
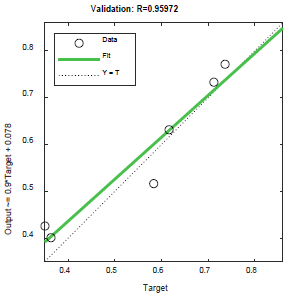
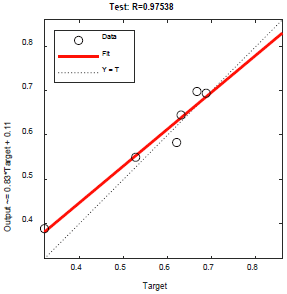
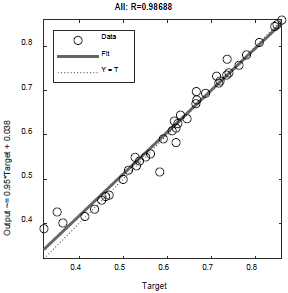
圖3 神經網絡訓練結果

圖中R=0.99954，十分接近于1，表明訓練結果具有很好的擬合性。往后研究如需要再提高預測精度，可通過增加預測數據集的方法。

由于電力機車類型、運行環境等條件都存在差異，因此機車撒砂量的范圍也會因條件不同而改變。為滿足機車制動、起步、爬坡等功能要求，撒砂器的撒砂量需要保證在300~700 mL/min范圍內，機務段使用砂子的密度范圍為1 500~2 000 kg/m³，因此撒砂器的撒砂質量范圍為0.40~1.4 kg/min^[10]。根據層次分析法計算出的結果，可將列車撒砂檔位分為三檔。當結果小于0.25時，電力機車撒砂裝置撒砂檔位取一檔，撒砂量取0.4~0.65 kg/min。當結果在0.25~0.50 時，檔位取二擋，撒砂量取0.65~0.90 kg/min。當結果在0.50~0.75 時，檔位取三擋，撒砂量在0.90~1.15 kg/min。當結果大于0.75 時，檔位取四檔，撒砂量取1.15~1.40 kg/min。

5   結語

本研究采取基于層次分析算法和神經網絡的方法解決因列車撒砂量過多引起的輪對損壞、粉塵污染或撒砂量過少，增黏效果無法滿足運行要求等問題。引入層次分析法，將加速度、速度、蠕滑速度、列車級位等因素綜合納入列車撒砂量評價體系，避免單一因素或者人工經驗多列車撒砂量的錯誤估計。引入神經網絡對數據信息進行分析處理，簡化了數據計算過程，方便在線計算。最終通過運算的結果對列車撒砂裝置撒砂量設定了四級不同擋位，以此來最大程度確定最佳撒砂量。

參考文獻：

[1] 譚江.高速輪軌黏著特性及增黏措施試驗研究[D].成都:西南交通大學,2019.

[2] 吳兵.高速輪軌黏著特性數值與實驗研究[D].成都:西南交通大學,2015.

[3] 邵軍.機車撒沙與提高黏著牽引力關系試驗研究[J].鐵道機車車輛,2016,(06):39-41.

[4] 文小康,黃景春,康燦.基于模糊控制的電力機車智能撒砂[1]控制方法[J].鐵道科學與工程學報,2019,(09):2304-2311.

[5] 王飛寬,徐紹龍,賓川,張征方.層次分析法在“神華號”八軸電力機車撒沙控制中的應用[J].機車電傳動,2017,(01):35-40+64.

[6] 鄧雪,李家銘,曾浩健等.層次分析法權重計算方法分析及其應用研究[J].數學的實踐與認識,2012,(07):93-100.

[7] 申鵬.輪軌黏著特性試驗研究[D].成都:西南交通大學,2012.

[8] 廖紅強,邱勇,楊俠,王星剛,葛任偉.對應用層次分析法確定權重系數的探討[J].機械工程師,2012,(06):22-25.

[9] 李世琛.基于MATLAB的幾類神經網絡穩定性分析仿真系統設計[D].青島:中國海洋大學,2013.

[10] 陽吉初,劉智遠,翟方志等.基于氣固兩相流的撒砂器結構設計方法[J].電力機車與城軌車輛,2016,(05):39-42.

（本文來源于《電子產品世界》雜志2022年4月期）