0   引言

異步電動機以其結構簡單、制造成本低等優點被廣泛應用。斷條故障是異步電機最常見的故障之一，約占10%，電機的頻繁啟動、集膚效應等因素都會引起轉子導條斷裂，如果不及時發現故障，會導致其他導條應力增加發生斷裂，機器損壞進而導致大規模損失^[1]。因此，對異步電機進行早期的運行狀態檢測是十分必要的。傅里葉變換的電機電流特征分析（MCSA）是最廣泛使用的方法，將時域中很難觀測到的信息在頻域中有很好的體現，但不適用于分析非平穩和非線性信號。文獻^[2-3]使EMD 的時頻域分析方法，可以將定子電流信號進行有效分解。但是在分解時，會出現模態混疊問題。

因此，在EMD 基礎上，提出了基于完全互補小波噪聲輔助集總經驗模態分解（CCWEEMDAN）算法[4]的斷條故障診斷方法，以下簡稱C 算法。C 算法能夠有效克服EMD 算法中的模態混疊問題，將噪聲信號更好地分離出來，得到更好的模式分量。它分兩步發生，第1 步是通過添加高斯白噪聲的方式對多分量信號進行分解，將信號分解為各含有不同信號頻率的本征模態函數（IMF）。第2 步，這些分解得到的模式分量信號調制解調，從而提取出故障特征頻率。

1   基本理論

1.1 斷條故障機理

感應電機正常運行時，轉子轉速為n ，轉差率是s ，定子電流只含有頻率為f1 的基波分量，定子旋轉磁場的速度為n1 ，轉子電流頻率為sf1 ，轉子旋轉磁場相對于轉子的速度為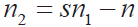 ，轉子旋轉磁場相對于定子旋轉磁場是靜止的，電機中只存在正向旋轉磁場。如果出現斷條故障，則轉子電路不對稱，轉子電流的對稱性被破壞，產生不對稱的轉子磁場，可分為正向和反向旋轉磁場。正向旋轉磁場和原定子磁場保持同步，它們的相互作用產生與普通感應電機相同的電磁轉矩。但反向旋轉磁場的旋轉方向與轉子相反。它相對于轉子的速度是，相對于定子的速度是n3 = n ? sn1 = (1? 2s)n1。并且在定子繞組中感應出電動勢和電流，頻率為（1-2s) f1^[5]。這種電流與基本氣隙磁通相互作用產生2sf1 的諧波，這種現象會在給定的頻率上產生一系列額外的電流分量：

f_rb為邊帶頻率， k =1, 2,3... ， s 為異步電機轉差率。

n_s 為同步轉速， n 為轉子轉速。

當時，邊頻帶分量（1± 2s) f1 是最明顯的邊頻成分，是用來識別斷條故障的重要依據。

1.2 完全互補小波噪聲輔助集總經驗模態分解原理

EMD 算法可以適用于非平穩信號，在分解中會出現模態混疊問題。集總經驗模態分解（EEMD）^[4]在EMD 基礎上給原信號添加高斯白噪聲可以有效抑制模態混疊，但會存在偽模態問題。為了克服EEMD 中的問題，互補集總經驗模態分解（CEEMD）^[4]在原信號添加互補高斯白噪聲，但會出現基頻模態偏差問題。因此提出了C 算法，通過在每階模態分解中添加互補的經小波變換分解重構的噪聲，可以有效地解決上述問題。在C 算法中，定義Wj(●)算子為信號進行小波變換重構后第j個細節信號，M(?)算子為經過EMD 分解后的一階模態的殘差。

1）通過小波變換對噪聲信號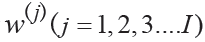處理然后重構第一個細節信號，得到W₁(ω^(j))。

此時，x^(j)= x +β₀W₁(w^（j）) ( j = 1, 2,3...I / 2)，x( j+I /2) = x ?β0W I 1(w( j) ) ( j = 1, 2,3... / 2)，其中I為待構建信號數量。對上述信號再進行EMD 分解后可以得到I 個殘差。平均后第一階數殘差：

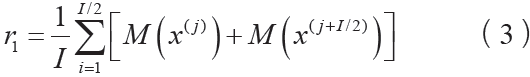
2）計算第一個模態分量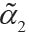=x?r₁。

3）對上述殘差增加噪聲信號β₁W₂(w^{( j)})，得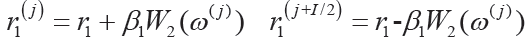， 經過EMD 分解后獲得第二階殘差：

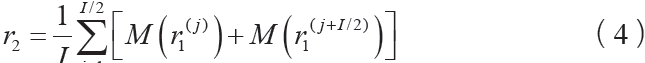
5）同上述原理，當k = 3, 4,5... ，可，得到第k 階殘差：

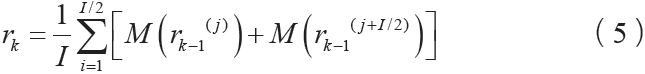
6）第k 階模態分量。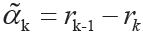

7）返回步驟5，計算下一個模態分量。

上述C 算法步驟，如流程圖1 所示：

為了驗證此算法的分解效果，構造一個仿真信號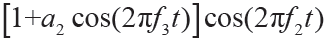， 其中a₁ = 0.05 a₂ = 0.02 ，f₁ = 100 ， f₂ = 50 ， f₃ = 3，0≤t≤2。其中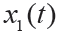二次諧波分量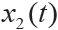，為基頻分量的調制信號。仿真信號及其組成部分如圖2 所示，利用C 分解和EMD 分解如圖3和4 所示。

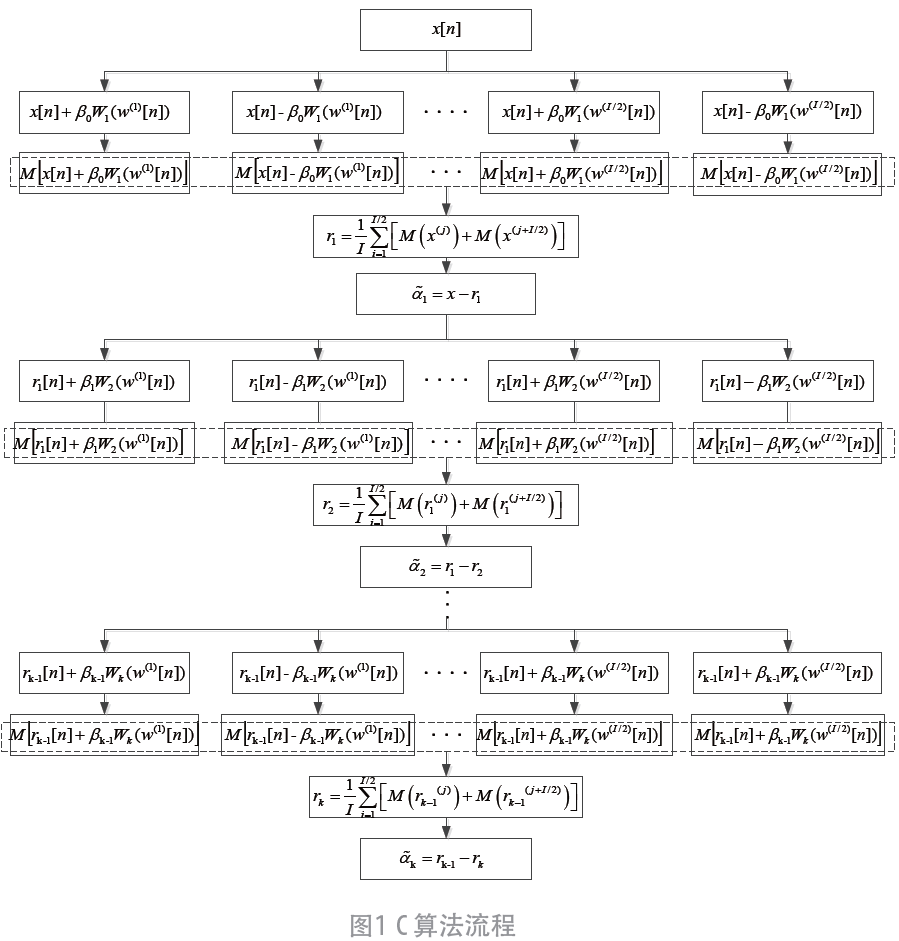
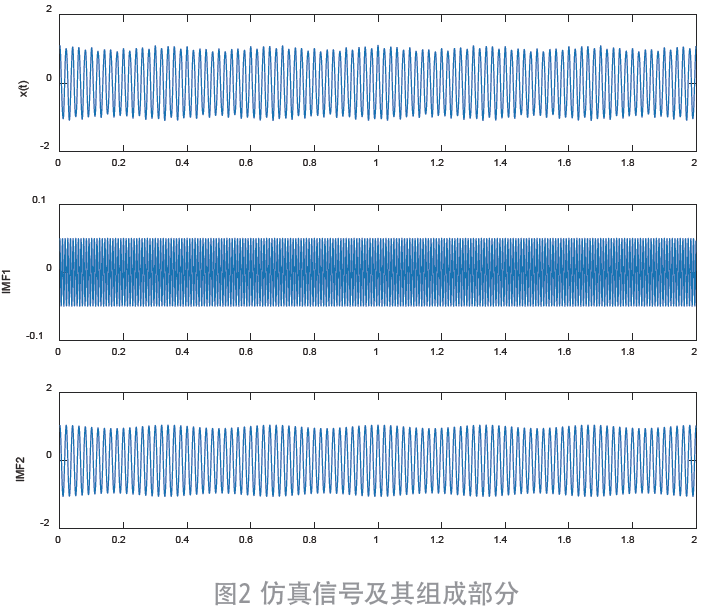
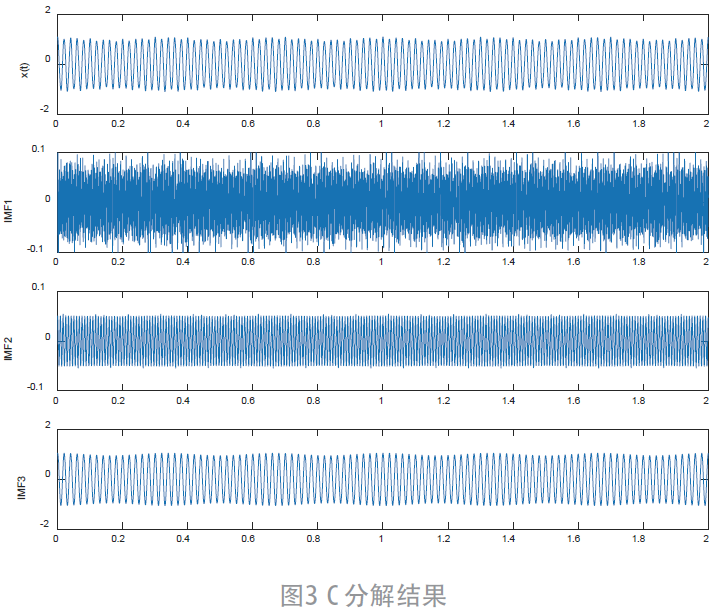
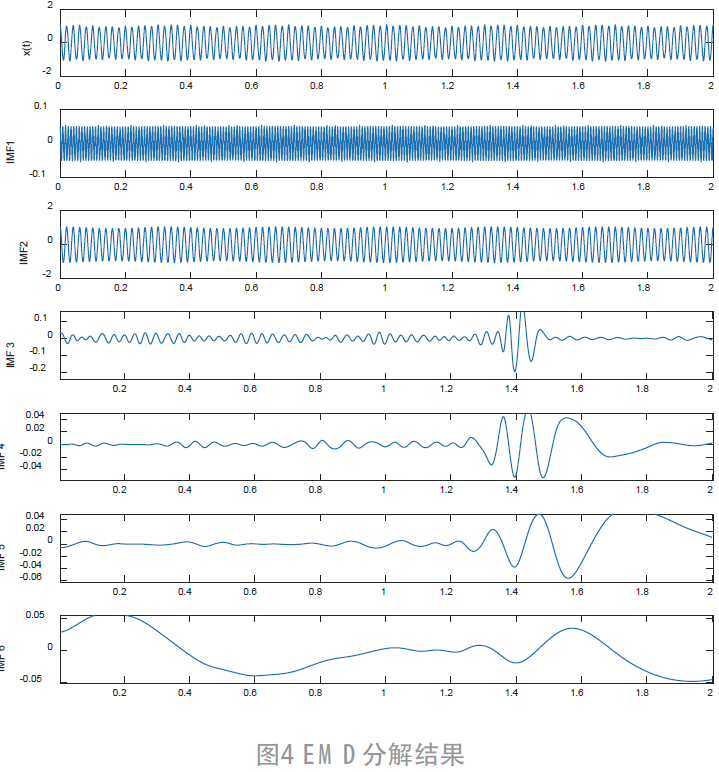
對比3、4 圖可知，無論是EMD 還是C 算法都可將原始信號分解成從高頻到低頻的各個分量。可以看出，EMD 分解的信號具有嚴重的模態混疊問題，含有多個不同頻率分量，信號分解效果較差。C 算法通過添加高斯白噪聲有效解決了模態混疊問題，圖3 中IMF1 為噪聲信號，IMF2 為二次諧波信號，IMF3 為基頻分量調制信號，可以發現，C 算法能比較準確地分解出原始信號。由此可見，應用C 算法對于提取信號具有可行性。

2   基于C算法的斷條故障特征提取方法

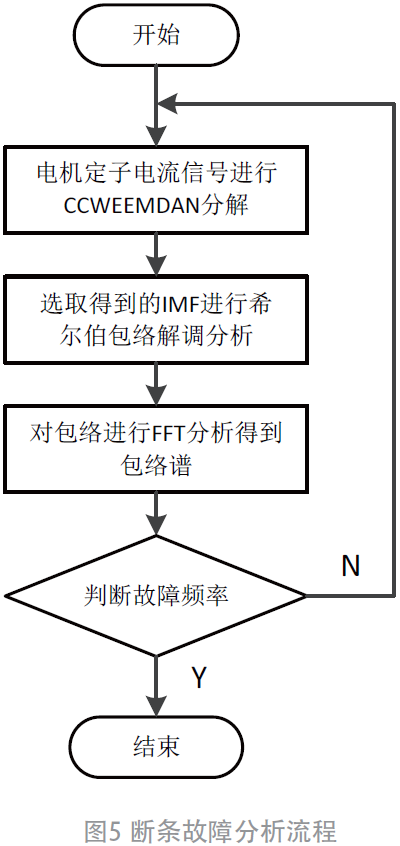
對收集到的定子電流信號先經過C 算法分解，將原始信號分解為從高頻到低頻的各個本征模態函數，進而對分解信號希爾伯特調制解調，在此基礎上進行FFT分析，得到包絡譜，精確的提取出故障頻率特征，流程如圖5 所示。

1）對收集的電機定子電流信號使用C 分解，將電流信號分解成各個含有不同頻率特征的IMF。

2）利用希爾伯特變換濾波特性進行調制解調，得到解析信號和包絡信號。

3）使用FFT 將信號轉化到頻域中，得到信號包絡譜，提取故障特征頻率。

4）觀察包絡譜中的特征頻率并與理想邊帶頻率2sf1 進行對比，判別故障頻率。如若不是則從1）開始。

3   異步電機斷條故障實驗驗證

為了驗證上述方法的有效性，以異步電機斷條為研究對象，該數據來自巴西S?o Paulo（USP）大學S?oCarlos 工程學院過程與系統智能自動化實驗室和電機智能控制實驗室。

感應電機各參數為：0.75 kW，220 V-3.02 A/380 V-1.75 A，4 極，60 Hz，額定轉速1 800 r/min，額定轉矩4.1 N·m。

選取實驗負載為2.5 N·m（負載率62.5%）時，不同電機狀況運行下數據。

健康電機定子電流C 分解如圖6 所示：

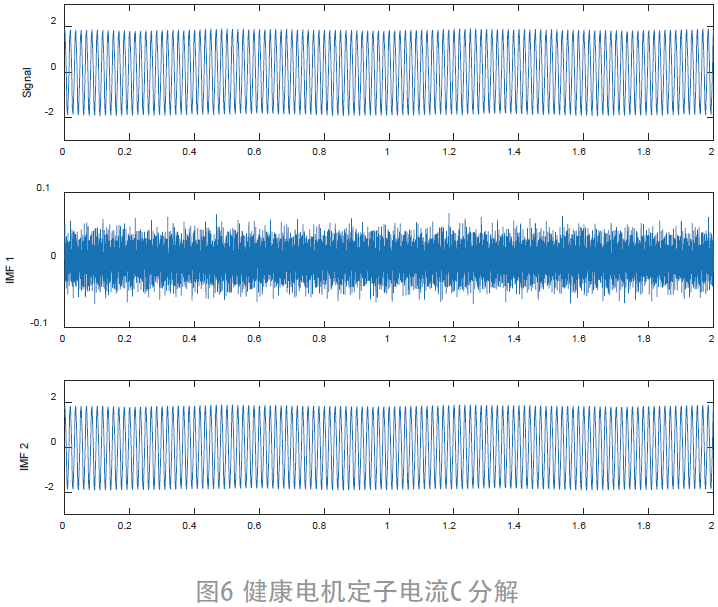
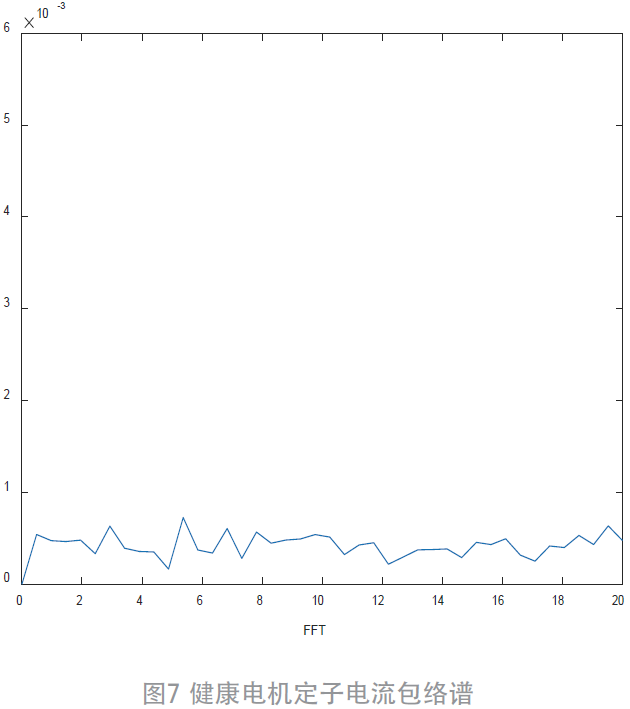
因此對IMF2 進行調制解調和FFT 得到包絡譜如圖7 所示。

電機一根斷條定子電流C 分解如圖8 所示：

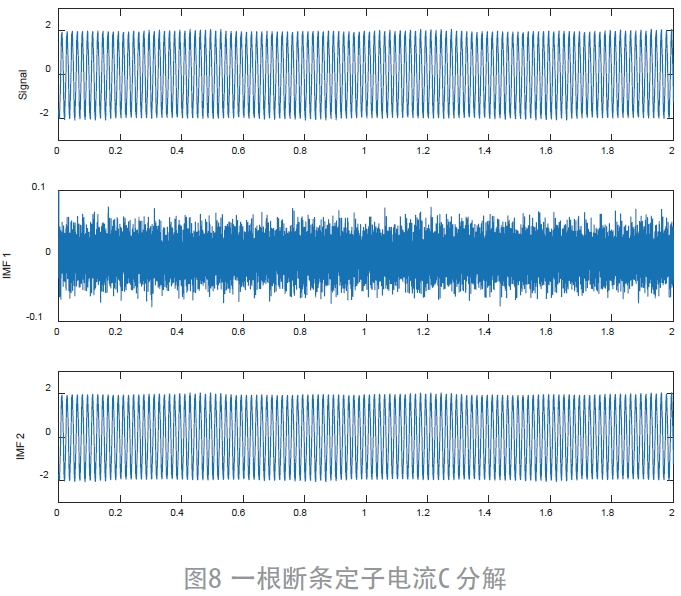
對IMF2 進行包絡解調和FFT 后得到包絡譜如圖9所示：

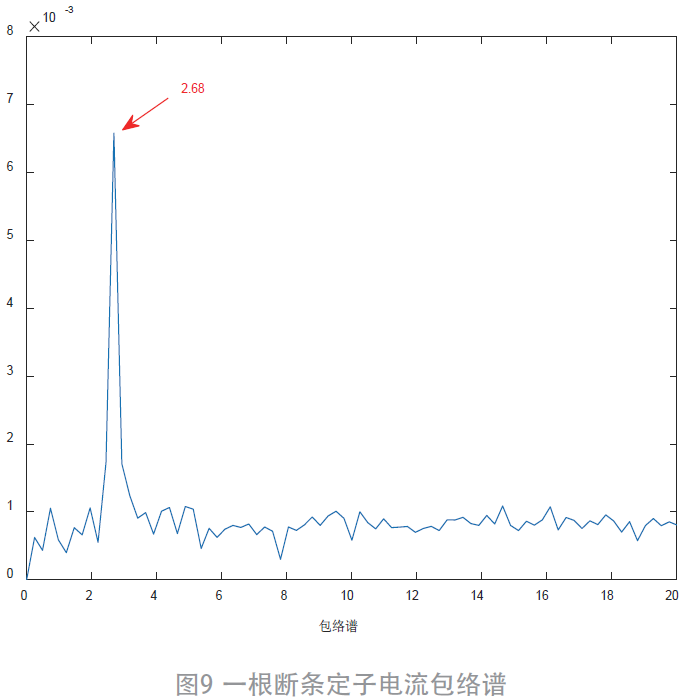
由圖6 和圖8 可以發現，經過C 分解后，有兩個模式分量。IMF1 為原始信號中的噪聲與添加的噪聲信號，IMF2 為得到的所需信號，因此對IMF2 進行后續處理。圖7 和圖9 包絡譜圖顯示，健康電機狀態時，并不會有任何明顯的故障頻率出現。但由于電機在制作材料裝配中存在的一些問題，依舊會有一些很小的邊頻成分存在，這是不可避免的。電機發生一根斷條故障時，可以發現有一個明顯的故障特征頻率2.68 Hz 成分。對比負載轉矩為2.5 N·m，轉差率s = 2.3% 時，理想故障特征頻率2sf1 = 2.76 Hz 可知，圖9 中的2.68 Hz 就是對應的故障特征頻率。由此驗證了運用此方法是可以有效提取出故障特征頻率。

4   結束語

以三相異步電機定子電流為研究對象，運用了C 分解的信號處理方法，通過調制解調和FFT 對斷條故障進行診斷識別。方法重點在于使用C 算法將定子電流數據分解為含有不同頻率成分的本征模態函數，通過調制解調得到模態函數的解析包絡信號，利用傅里葉變換提取到包絡譜，實現了故障診斷識別的目的。相比單純使用頻域分析FFT，可以有效提取故障特征頻率，同時使用改進EMD 的C 算法處理數據能有效避免EMD 算法中存在的模態混疊，得到更好的模式分量，對于數據的處理更好，在實際在線監測異步電機斷條故障診斷中具有很大的應用前景。

參考文獻：

[1] GANGSAR P,TIWARI R.Signal based condition monitoring techniques for fault detection and diagnosis of induction motors:A state-of-the-art review[J].Mechanical systems and signal processing,2020,144.

[2] Valles-Novo R,Rangel-Magdaleno J,Ramirez-Cortes H.et al.Broken bar detection on squirrel cage induction

motors with MCSA and EMD[C].2014 IEEE International Instrumentation and Measurement Technology Conference(I2MTC) Proceedings,2014:993-998.

[3] YIGUANG C,HONGXIA Z,YONGHUAN S.Method of EMD and ZOOM-FFT to detect the broken bars fault in induction motor[C].2010 international conference on electrical machines and systems,2010:1387-1391.

[4] 何劉,丁建明,林建輝,等.完全互補小波噪聲輔助集總經驗模態分解[J].振動與沖擊,2017,36(4):232-242.

[5] Treml A E,Flauzino R A,Brito G C.EMD and MCSA improved via hilbert transform analysis on asynchronous machines for broken bar detection using vibration analysis[C].2019 IEEE Milan powertech,2019:1-6.

（本文來源于《電子產品世界》雜志2021年10月期）