程學農(中電海康集團無錫研究院，江蘇?無錫?214061)

　　摘?要：介紹了通過史密斯圓圖進行阻抗匹配使信號有效的傳輸到負載，本文著重于RFOUT與天線之間的匹配。NB-IoT模塊提供1個RF天線PAD供天線使用，通過使用電容和電感等元器件組成π形匹配電路，用于調節天線端口的性能，線路阻抗保持在50 Ω左右。通過對負載阻抗進行歸一化，畫出其圓。負載阻抗的實數部分與阻抗圓和導納圓有2個交點，其對應的x值為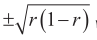的x值與負載阻抗的x值之差，所以兩者的差為匹配網絡需要串入歸一化電抗值，通過還原，可得串聯元件值，同理，通過導納圓可求得所需并聯元件值。

　　關鍵詞：反射系數；負載阻抗；特征阻抗；史密斯圓圖駐波比

　　0 引言

　　NB-IoT (窄帶蜂窩物聯網)聚焦于低功耗廣覆蓋（LPWA）的物聯網市場，是一種可在全球范圍內廣泛應用的新興技術。具有覆蓋廣、連接多、速率低、成本低、功耗低、架構優等特點，未來將會大規模地普及。因此隨著NB-IoT模塊的應用和發展，如何快速有效地對其應用設計成為了關鍵。現階段，市面上多數NB-IoT模塊的使用都較簡單，采用UART進行數據傳輸，所以應用設計的關鍵點在于天線部分。通常，合格的RF電路通常反射系數小于1/3，為了使電路的發射系數在一個合格的范圍內，需通過阻抗匹配的方法來實現。

　　通常實現阻抗匹配的方法可以分為四大類：①計算機仿真；②手工計算；③經驗；④史密斯圓圖。計算機仿真使用的前提是需要對其原理較精通；如不精通，容易在參數設置上發生錯誤。手工計算的缺點是較繁瑣，需要大量的計算量，耗費時間。通過經驗的辦法也有著較大的局限性，不適合所有人。面對以上方法所呈現出的缺點，史密斯圓圖可以在不作任何計算的前提下得到一個精確的阻抗匹配，避免繁瑣的計算過程。借助史密斯圓圖可以用圖解法解出天線阻抗的匹配網絡，其精準度與史密斯圓圖的精度相關。

　　1 阻抗匹配

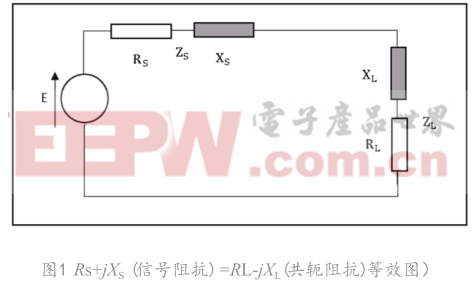
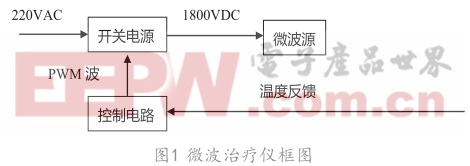
　　天線和饋線的連接處稱為天線的輸入端，天線輸入端的電壓與電流的比值稱為天線的輸入阻抗，表達式為R jX + ，其中實數部分為輸入阻抗( R )，虛數部分為輸入電抗(Xi)。天線的匹配就是消除天線輸入阻抗中的電抗分量，使電阻分量盡可能地接近饋線的特性阻抗。阻抗匹配的目的是使功率最大化，避免能量從負載反射回信號源，以及避免頻率牽引現象的產生 ^[1] 。阻抗匹配的方法是在負載和源之間構造一個匹配網絡，是其阻抗等于負載的復阻抗的共軛，如圖1所示。

　　2 反射系數

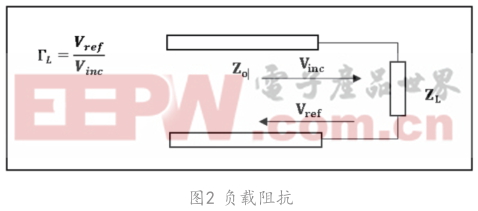
　　信號不能區別什么，能感受到的只有阻抗。如果信號感受到的阻抗是恒定的，此時信號正向傳播。如果阻抗發生了變化，信號就會產生反射。衡量反射量的指標為反射系數，反射系數為單端口散射參數（S-parameter）里的S11 ^[2] ，是歸一負載值，是發射電壓與傳輸電壓之間的比值，其表達式為：

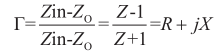　　(Z _O為特征阻抗，為實數）

　　假設1：PCB線的特征阻抗為50 Ω，如果遇到一個200 Ω的貼片電阻，不考慮寄生電容電感的影響，那么反射系數為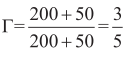，意味著信號有3/5被反射回源端。在RF電路中，反射系數越接近0越好，絕對值要小于1/3。

　　假設2：終端接負載阻抗 Z _L = 125+50j ，那么反射系數為:

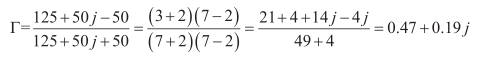
　　駐波比VSWR=3.04

　　當VSWR=1時，表示完全匹配，實際應用中，VSWR要小于1.2。所以上述情況為失配。通常，匹配的程度可以通過反射系數、行波系數、駐波比和回波損耗這幾個參數來進行衡量。

　　3 使用史密斯    圓圖進行阻抗匹配

　　3.1 史密斯圓圖介紹

　　已知反射系數Γ的表達式:

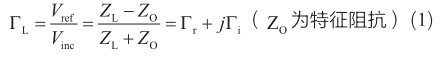
　　因為 Z _O 是一個實數，因此可以將其固化

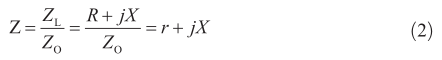
　　通過式(1)和式(2)，可以得到：

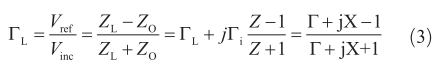
　　通過式(3)可以得到：

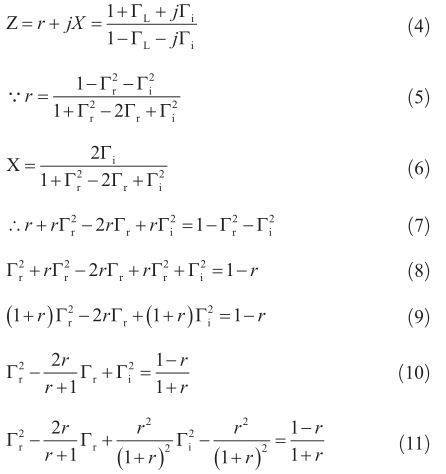
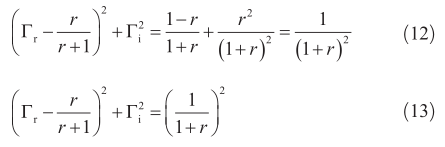
　　經過整理，最終得到式(13),可以理解為在復平面

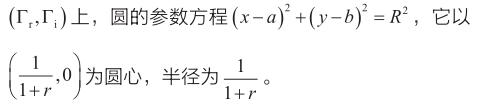
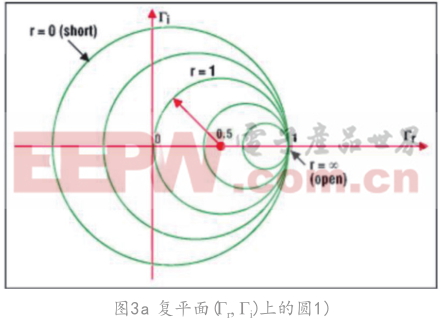
　　圖3a表示圓周上的點具有相同實部的阻抗，如r =1的圓，表明(0.5, 0)為圓心，半徑為0.5。它包含了代表反射零點的原點(0, 0)。以(0, 0)為圓心、半徑為1的圓代表負載短路。負載開路時，圓退化為一個點(以1, 0為圓心，半徑為0)。

　　同理，通過式(5)和式(6)可推導出：

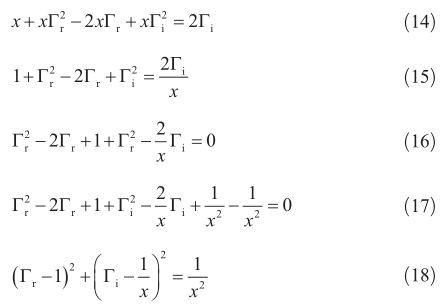
　　式(18)表明了在復平面( Γ _r,Γ_i )上的圓的參數方程 (x-a)²+(y-b)²=R²，它的圓心為( 1,1/ x )，半徑1/ x。

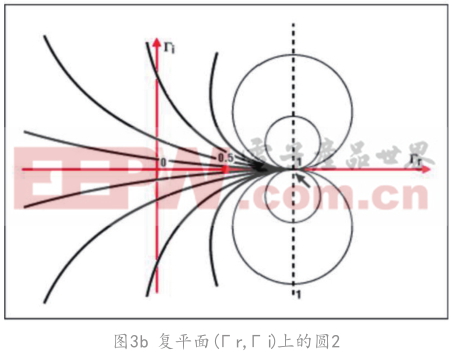
　　同理，圖3b表明了圓周上的點有相同虛部 x 的阻抗。所有的圓(x為常數)都包括點(1, 0)。與實部圓周不同，x的值可為正或負，復平面下半部是其上半部的鏡像。將兩簇圓周放在一起。可以發現一簇圓周的所有圓會與另一簇圓周的所有圓相交。因此，假設已知阻抗為r+jx，只需要找到對應r和x的兩個圓周的交點就可以得到其反射系數。

　　舉例如下。

　　(1) 已知特性阻抗為50 Ω，負載阻抗如下：

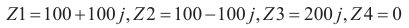
　　(2) 對負載阻抗進行歸一化

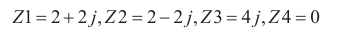
　　(3) 通過原圖中的直角坐標或者極坐標可以讀出其發射系數（圖4a和圖4b）

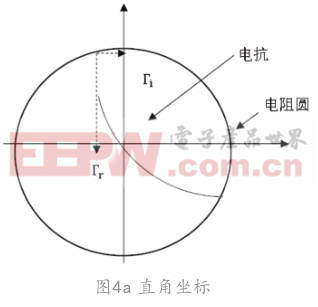
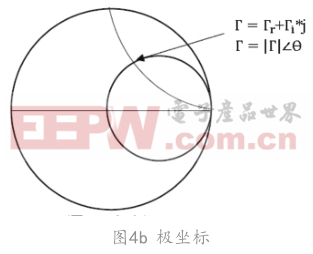
　　(4)在史密斯圓圖上顯示其坐標(如圖5)

　　(5)在圓上讀出反射系數、駐波比及回波損耗

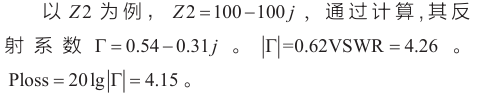
　　畫圖法：連接圓心到負載點 Z2 ，以這條直線為半徑，實軸中點為圓心畫圓，在圓與實軸左邊的交點上畫圖一條直線，讀出值（如圖6）。

　　3.2 如何串并電感電容

　　圖7中間的水平線為純阻抗線，水平線上的點表明純電阻。實軸上半平面(x < 0)是感性阻抗的軌跡，實軸上下平面(x > 0)是容性阻抗的軌跡，在上方的點用電路表示可認為是1個電阻串聯1個電感，在下方的點則為1個電阻串聯1個電容 ^[3] 。圓則代表等阻抗線，指落在上面的點的阻抗都相等。因此，可以在圖8表示出來。

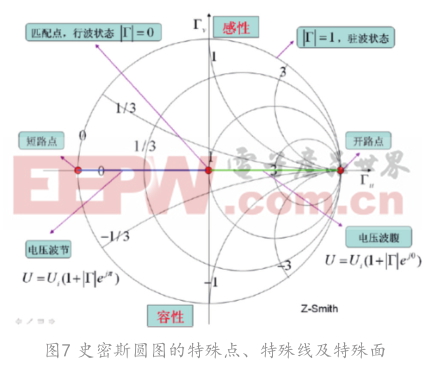
　　串聯電感：阻抗原圖中等電阻圓上順時針旋轉；

　　并聯電容：阻抗原圖中等電阻圓上逆時針旋轉；

　　并聯電感：導納圓圖中等電導圓上逆時針旋轉；

　　并聯電容：導納圓圖中等電導圓上順時針旋轉；

　　3.3 N B-IoT 模塊實際案例：

　　3.3.1 N B-IoT 天線匹配網絡

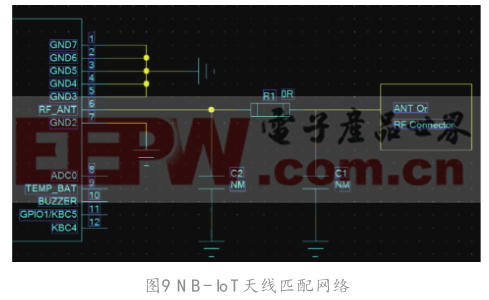
　　以圖9為例，模塊提供1個RF天線PAD供天線使用。C1、C2、R2三個元器件組成 π 形匹配電路，用于調節天線端口的性能。通常情況下，在PCB布線時，為了防止信號反射線路阻抗盡量保持在50 Ω左右。為了減少計算量以及復雜程度，首先可以考慮先使用電容和電感進行匹配。過程如下。

　　NB-IoT模塊的發射頻率為900 MHz，天線阻抗Z=60+50j ，饋線阻抗W=50 Ω。

　　(1) 歸一化：

　　(3)選擇一個交點J1：0.91?b=0.5 - (-0.41)=0.91

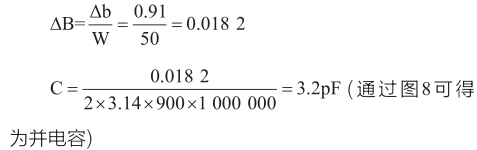
　　(4)求交點的對稱點（阻抗）的值

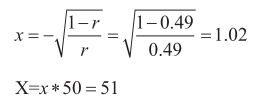
　　(5)求串聯元件值

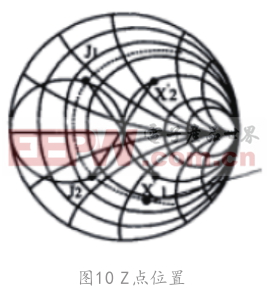
　　(6)對應網絡圖（圖11）

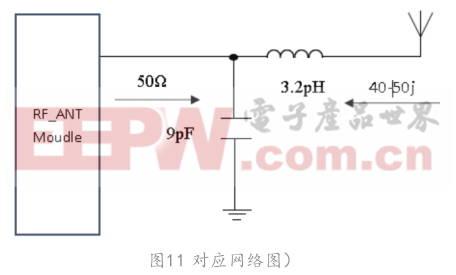
　　(7)同理，可以計算第2個交點，方法相同。3.4 π形網絡（圖12）

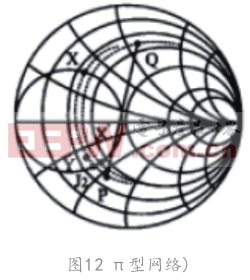
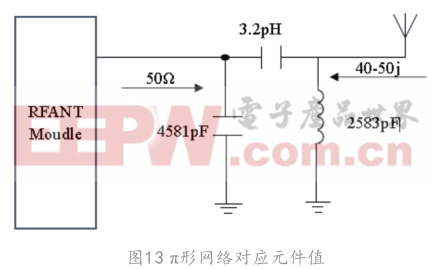
　　當交點J2與Y點的差值較小時，Y點越過J2點繼續向下移動至P點，此時我們可以通過上述的辦法進行π形網絡的匹配。

　　(7)對應π形網絡如圖13

　　4 總結

　　上述例子講述了NB-IoT天線匹配網絡的操作過程，通過史密斯圓圖，可以直接讀出電路的反射系數、駐波比等參數，減少繁瑣的計算，提高效率。當反射系數覺得值小于1/3可認為此電路合格。當反射系數大于1/3，通過對其進行串并電容，電感進行阻抗匹配，直至反射系數小于1/3為止。如需更精準的匹配，則可通過計算機仿真等其他方式來進行阻抗匹配。

　　參考文獻：

　　[1] 陳俊夫.對于Smith圓圖的應用和理解[J].中國新通信, 2015(17):48-48.

　　[2] 杜廣超.史密斯圓圖在天饋系統中的應用[J].科技風,2012(4):73-73.

　　[3] CHAN K C.利用史密斯圓圖設計匹配網絡[J].無線電工程,2001, 31(12):51-53.

　　[4] 王延平.利用smith圓圖快速求解阻抗匹配網絡[J].有線電視技術,2013,(12):95-98.

　　[5] TORUNGRUENG D,THIMAPORN C.A generalized ZYSmith chart for solving nonreciprocal uniform transmission‐line problems[J]. Microwave and Optical TechnologyLetters,2004,40(1): 57-61.

　　（注：本文來源于科技期刊《電子產品世界》2020年第06期第76頁，歡迎您寫論文時引用，并注明出處。）