機器學習定義：A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E(一個程序從經驗E中學習解決任務T進行某一任務量度P，通過P測量在T的表現而提高經驗E(另一種定義：機器學習是用數據或以往的經驗，以此優化計算機程序的性能標準。)

　　不同類型的機器學習算法：主要討論監督學習和無監督學習

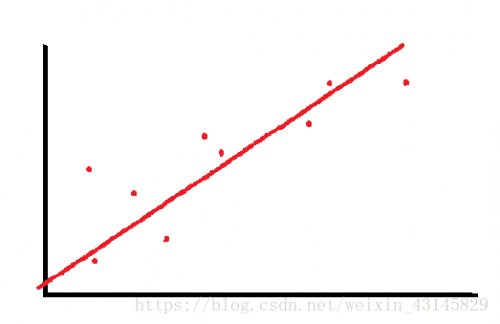
　　監督學習：利用一組已知類別的樣本調整分類器的參數，使其達到所要求性能的 過程，也稱為監督訓練或有教師學習。(樣本有明確的標簽和定義，數據間有明確的邏輯關系。通過已有的數據來預測未知的數據。)，主要涉及回歸問題和分類問題。

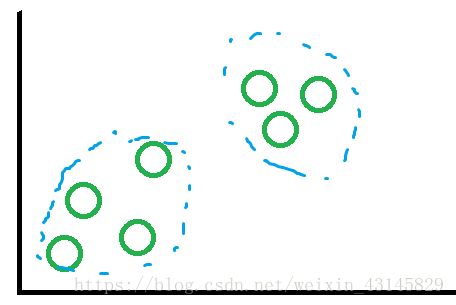
　　無監督學習：根據沒有標記的數據樣本識別各種問題。典型例子是聚類算法。

　　1.線性回歸問題

　　設計一個函數，使它盡量滿足我們所給出的數據(訓練集，可能有很多個特征，這里簡化假設只有一個特征也就是只有一個變量x，我們假設給出m組數據*)，并可以對數據做出可信的預測。

　　如果我們的假設函數設為

　　hθ(x)=θ0+θ1x，此處的θ為模型參數，選擇不同的θ0和θ1能夠得到不同的函數圖像。現在如何得到最能夠擬合數據的一組θ0和θ1呢?

　　這個“最能擬合數據”可以理解為對每一個x，其預測值與真實值，也即

　　|hθ(xi)-yi| 最小，我們引入一個代價函數 J(θ0，θ1)：

　　J(θ0，θ1)=1/2m∑(hθ(xi)-yi)^2

　　可以看出，我們的目的就是找出最適合的θ0和θ1，使代價函數J(θ0，θ1)的值最小。

　　要找出這個最小值，我們可以采用一種梯度下降的方法，在此之前，先得更深層次地理解代價函數。

　　我們先忽視θ0，那么代價函數是關于θ1的函數，要找出其最小值，通過圖像可以看到：

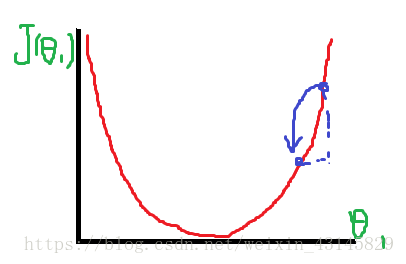
　　θ1取中間那一點就是我們所求值。我們可以從其他的點不斷”逼近“最低點，具體操作為：

　　不斷更新θ1：

　　θ1：=θ1-α/θ1*J(θ1)

　　后面那一項是J在θ1這一點的偏導數。可以理解為將θ1向其斜率方向偏移一點點，由于J(θ1)不斷減小，偏移量也不斷減小。這樣隨著不斷更新，我們可以得到最終結果。

　　現在如果我們在引入θ0，那么代價函數是關于兩個變量的函數，所成的圖像是一個曲面，同樣要找到”最低點“，應對兩變量同時進行上面的更新。

　　同樣的，如果特征量非常多，J是有關n個變量的函數，同樣沿用上面的方法。

　　梯度下降的幾個注意點：

　　更新式子的α可以理解為下降的”“步幅”，但α過小會導致回歸速度很慢，需要更新多次。而α過大會導致無法達到最低點，在更新一次后可能越過最低點。

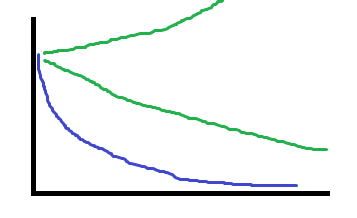
　　α(稱為學習率)的選取可以觀察(更新次數)~J的圖像。

　　藍色的曲線表示所取的α較合適，下面的綠色表示α過小，上面的綠色表示α過大。

　　對于θ的更新，式子可以展開簡化為

　　*θi=θi-1/m∑(hθ(xi)-yi)xi

　　(i=0，1，2，3···n)其中x0=1;

　　特征縮放。對于有多個特征的數據，如果各個特征的范圍比較接近，梯度下降法可以更快的收斂。

　　執行時更一般地將特征約束到-1到1之間。可以用這個式子：

　　xi=(xi-μi)/si其中μ為特征x的平均值，s為特征x的范圍。

　　正則化問題。實際問題中一個結果可能和多個特征有關，如果特征過多，而訓練數據較少，為了強行滿足所有的數據，會出現“過擬合”現象：

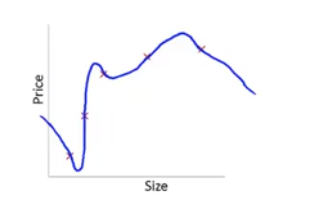
　　解決方法是盡量去掉不必要的特征量，或者進行正則化，將所有特征量減小(一般不包括x0)。

　　J(θ)=1/2m[∑(hθ(x)-y)2+λ∑θ 2](后面加的稱為懲罰項)要讓這個式子盡量小，那么θ就要盡量小，以此達到減小θ的目的。

　　將這個修改后的代價函數帶入更新式。

　　θ=θ(1-αλ/m)-a/m∑(h(x)-y)x

　　這會使曲線相對平滑。正則化參數要設的大一點，但如果太大的話所有θ相當于不存在，曲線就會成一條水平直線。

　2,分類問題

　　在分類問題中，我們簡化模型為只有兩個分類0和1.但數據的范圍遠在0至1之外，所以我們可以用logistic函數做處理：

　　h(x)=1/(1+e-fθ(x))

　　z為0時g(z)取0.5，g(z)在0到1之間

　　這樣就可以將正負改為與0.5的大小區別，實際上h(x)=P(y=1|x;θ)

　　即得到的結果可以代表y為1的概率

　　這樣當h(x)>0.5時我們可以認為對應的xi分類為使y為1，h(x)<0.5認為對應的xi使y為0。

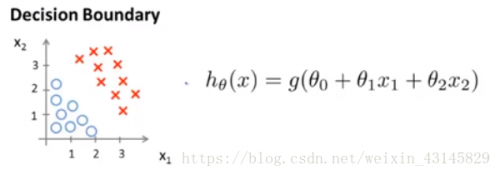
　　如圖的h(x)將數據分為兩部分，這條線叫做決策邊界。在線內外的數據位置分別對應著與零的大小，概率表現在h(x)上。當然決策邊界可以是不同形式的函數。