1 引言

在密碼學領域，利用密碼技術|0">密碼技術對傳輸信息進行加密發送、解密接收，是一種行之有效的方法。密碼學發展至今已有許多優秀的算法發明并得到應用，例如私鑰密碼體制中的DES密碼、IDEA密碼、序列密碼；公鑰密碼體制中的RSA密碼、橢圓曲線密碼等，他們各有設計特點和對應的應用領域，其中序列密碼一直是密碼學中最重要的加密方式之一。利用組合LFSR序列作為序列密碼的前饋電路，可充分利用m序列的良好統計特性和加大輸出序列周期和線性復雜度的優勢，但如何在保證前饋電路輸出統計特性不被破壞的基礎上，置換與混亂輸出關系，增強密碼的保密性仍是該領域研究必須思考的問題。傳統方法是利用非線性函數對前饋電路輸出進行變換，但在函數設計與生成速度上制約了其發展；利用某LFSR序列產生控制信號去控制并行LFSR序列，這種形式電路如Geffe發生器、Jenning發生器、交錯停走式發生器等，易受到相關性攻擊，應避免在保密強度要求高的部門應用。隨著現代科學技術的發展，將神經網絡、混沌等算法融入密碼學的研究已不斷深入，伴隨著數字化技術和大規模集成電路的快速發展，一些算法不僅停止在理論研究與模擬仿真實驗上，利用硬件電路進行設計并實現已逐漸成為事實。如何衡量加密芯片的復雜度是應該研究的問題，當加密芯片被敵方得到并破譯時，以高復雜度保持加密信息的安全性是加密芯片成功設計的關鍵。現提出一種混沌組合序列密碼復雜度分析與設計方法，并由此設計混沌組合序列密碼電路并基于FPGA實現。

2 序列密碼原理

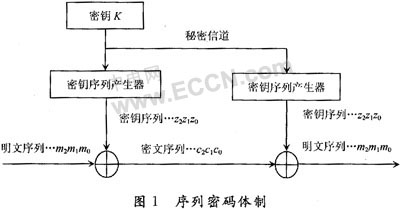
由于語音、圖像和數據等信息都可以經過量化編碼轉化為二進制數字序列或本身就是二進制數字的序列，因而可以假定序列密碼系統中的明文為二進制數字序列組成的集合m={mi}，密鑰空間為K，密文空間為C={ci}。如圖1所示，對于每一個k∈K，由算法Z可以確定一個二進制序列Z(k)=z0，z1，z2，…，當明文為m0，m1，m2，…，mn-1時，在密鑰k下的加密過程為：對i=1，2，3，…，n-1，計算ci=mi○+zi，密文為c=Ek(m)=c0，c1，c2，…，cn-1，對密文c的解密過程是：對i=1，2，3，…，n-1，計算mi=ci○+zi，由此恢復明文為m。通常，稱密鑰k為種子密鑰，由k通過算法Z產生的序列Z(k)稱為密鑰序列。

由此可見，序列密碼的安全性主要取決于密鑰序列Z(k)和序列密碼算法的難破譯性。當z0，z1，z2，…為均勻分布的二進制隨機序列時，則該密碼系統為一次一密系統，因此是不可破的。但是由于Z(k)是一個由k通過確定性算法產生的偽隨機序列，所以該密碼系統的保密性關鍵是高復雜度設計。

3 密碼芯片電路設計

根據國內外在混沌序列密碼研究的分析，本文設計了基于FPGA的混沌序列密碼芯片，該芯片核心部分是混沌序列密碼模塊，如圖2所示。加密芯片除混沌序列密碼模塊外還有控制模塊和加／解密傳輸模塊。

從該框圖可以看出，由8個LFSR序列作為驅動源，Lorenz混沌系統與數據選擇器Ⅰ構成對8個LFSR序列進行非線性變換部分，數據選擇器工輸出序列與數據選擇器Ⅱ輸出序列相異或后產生密鑰輸出序列。

選擇器根據Lorenz混沌系統選擇信號輸出，其中選擇器的控制端信號也來源于Lorenz混沌系統的任意一輸出。根據多個LFSR序列作為驅動源的特性得知，當LFSRi(i=1，2，…，n)的級數N1，N2，…，Nn兩兩互素且滿足一定條件時，該組合序列輸出周期為。為了使輸出序列有盡可能大的線性復雜度，各Ni應盡可能接近N／n，其中N=N1+N2+…+Nn。當Ni確定以后，為使每個LFSRi(i=1，2，…，n)生成周期為2Ni-1的m序列，其充要條件是使其特征多項式為本原多項式。

4 密碼芯片電路的復雜度分析

該結構輸出周期較單一LFSR作為前饋電路的輸出周期大大增加，同時此電路的復雜度大大增加，可從以下證明中得到。

該密碼電路中構成線性復雜度的主要器件有8個LFSR、混沌序列發生器及數據選擇器，設8個LFSR級數分別為Di(i=1，2，…，8)且互不相等，di(i=1，2，…，8)分別為8個LFSR的輸出，a0a1a2為Lorenz混沌序列輸出，設Y1(t)，Y2(t)分別為數據選擇器Ⅰ和Ⅱ的輸出，那么：

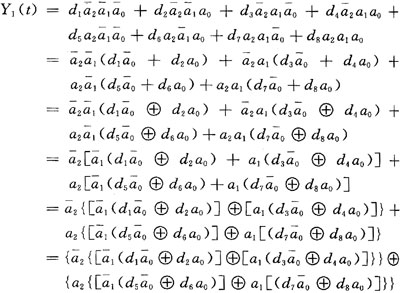
如果假設混沌每個輸出序列復雜度為A，LFSR的復雜度分別以他們各自級數表示，依據復雜特性基本定理，則Y1(t)的線性復雜度L1可由上面的邏輯輸出表達式計算為：

此式給出描述多控制端的數據選擇器線性復雜度的基本公式，可看出該電路線性復雜度主要由An項決定，如果LFSR數目增加，復雜度將為冪指數增長。

5 加密芯片電路輸出測試

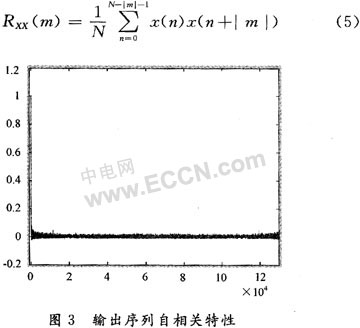
利用ALTERA公司的QuartusⅡ工具和目標芯片EP20K300EQC240設計，對邏輯綜合結果進行仿真后完成硬件下載功能。為驗證其輸出序列的平衡性、相關性及游程等特性，對下載后輸出序列利用Agilent1693A邏輯分析儀進行數據測試、存儲并利用Matlab進行統計分析。在實際應用中，如果平穩隨機序列滿足各態歷經性，統計均值可用時間均值代替。取一個有限的計算系統能夠承受的時間均值和時間自相關序列，并用他們作為統計均值和統計自相關序列的估值。根據此理論設定一初始數據，在一段時間內觀測其輸出序列的平衡性、游程性、自相關性及互相關性，基本滿足密碼序列輸出要求，現以自相關特性測試為例進行說明。

將混沌組臺序列轉化成X={x(n)|n=0，1，2，…，x(n)∈{-1，1}}，使序列輸出概率密度關于0對稱。取測試序列N=12×104，并利用自相關函數的估值式(5)進行仿真，得到該神經網絡序列的自相關特性如圖3所示。可看出該密碼序列輸出具有較好的自相關特性，在0值處峰值尖銳，其他值近似為0，類似于δ函數。

6 結 語

該電路的特點為：

(1) 單個混沌系統對多LFSR進行非線性變換，無限延拓多LFSR周期，在極大擴展了周期空間的同時，又增加了序列的復雜性；
(2) 由LFSR序列和混沌序列共同構建加密芯片電路的設計，避免由單一混沌序列而被重構的可能；

(3) 此電路的復雜性將高于單一混沌電路，更遠高于由LFSR組合序列生成電路；

(4) 該電路用FPGA技術進行設計，使硬件電路與數學算法有機結合一起，FPGA技術的特點使所設計電路易移植和更改，這對密碼的設計十分有利。

此加密芯片經VHDL設計并生成，整個時序由狀態機控制，邏輯關系符合電路設計要求。此研究結果有助于加快混沌序列密碼芯片的研究與應用，使加密算法更靈活有效地應用到信息安全和現代保密通信設備中。