摘要：首先利用RSA加密算法對數據進行加密和解密，實現了數據的安全傳輸;然后針對RSA加密算法時間開銷大和算法設計復雜的缺點，提出基于乘同余對稱特性的SNM算法。通過對該改進RSA加密算法的實現發現加密運算速度明顯提高且算法更簡單，從而證明了本文所提改進算法的有效性。

0 引言

在當今信息社會中，每天都有大量的加密信息在傳輸、交換、存儲和處理，一旦密碼遭到破解就可能造成信息的丟失、篡改、偽造、假冒以及系統遭受破壞等嚴重后果，因此，如何保證信息的安全傳輸成為當前信息傳輸領域的熱點問題。W.Diffie和M.E.Hellmam在1976年發表了具有劃時代意義的“密碼學的新方向”一文，提出了公鑰密碼體制思想，克服了傳統對稱密碼體制的缺點，為近代密碼學的發展指明了方向。它的出現是密碼學研究領域中的一項重大突破，也是現代密碼學誕生的標志之一。

本文首先對非對稱加密算法RSA的原理和優點進行研究，然后實現其加密、解密功能。RSA算法在公鑰密碼體制中占有重要的地位。但該算法所采用的冪乘計算耗時太多，一直是制約其廣泛應用的瓶頸。因此，為了提高加密和解密速度，本文提出一種新型的加密算法即基于乘同余對稱特性的SMM算法。該算法采用簡單的迭代來實現，不需要冪乘和乘法逆運算，從而在提高加密解密的速度同時也使得程序設計更簡潔緊湊。

1 RSA加密算法原理

RSA加密算法的理論基礎是一種特殊的可逆模指數運算，其算法描述如下：

(1)選擇兩個互異的大質數p和q(p和q必須保密，一般取1024位)。

(2)計算出n=p q，φ(n)=(p-1)(q-1)。

(3)選擇一個比n小且與φ(n)互質(沒有公因子)的數e。

(4)找出一個d，使得ed-1能夠被φ(n)整除。其中，ed=1 mod(p-1)(q-1)。

(5)RSA是一種分組密碼系統，所以公開密鑰=(n，e)，私有密鑰=(n，d)。

其中，n為模數，通信雙方都必須知道，e為加密運算的指數，發送方需要知道，d為解密運算的指數，只有接受方才能知道。

將以上過程進一步描述如下：

公開密鑰：n=pq(p，q分別為兩個互異的大素數)，e與(p-1)(q-1)互質。

私有密鑰：d=e-1{mod(p-1)(q-1)}。

加密：C=Me mod n，其中M為明文，C為密文。

解密：M=Cd(mod n)。

若要破譯密碼必須知道p，q，即對n作素因子分解，這在數學上是非常困難的。

2 RSA加密算法的實現

2.1 算法設計流程

RSA算法設計流程如圖1所示，主要采用下述加密/解密變換。

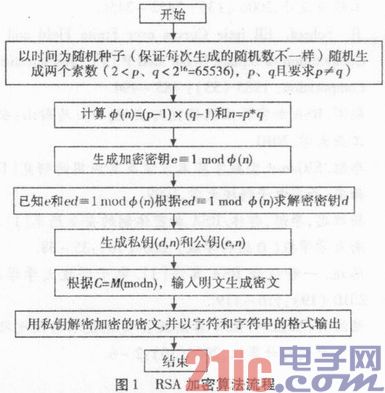
(1)密鑰的產生

a.選擇兩個保密的大素數p和q。

b.計算n=p q，φ(n)=(p-1)(q-1)，其中φ(n)是n的歐拉函數值。

c.選擇一個整數e，滿足1

d.計算私鑰d，滿足d=l(modφ(n))/e，d是e在模φ(n)下的乘法逆元。

e.以(e，n)為公鑰，(d，n)為密鑰，銷毀P，q，φ(n)。

(2)加密

加密時首先將明文比特串進行分組，使得每個分組對應的串在數值上小于N，即分組的二進制長度小于1 092 N。然后，對每個明文分組M，作加密運算。

加密：C=Me(modn)，其中M為明文，C為密文。

(3)解密

對密文分組的解密運算為：M=Cd(modn)。

2.2 RSA加密算法的實現

(1) 生成密鑰

隨機選擇兩個大素數p和q，如果p和q足夠大，那么n=p q就會變的很大，在理論上因式分解一個大數并準確地分解出p和q是很難實現的。本文隨機選擇P和q為61和67。根據φ(n)=(p-1)(q-1)可得n的歐拉函數值φ(n)為3960，如圖2所示。

隨機數e的選取要滿足隨機數和歐拉函數最大公約數gcd(eφ(n))=1這個條件。如果e比較大，加、解密速度變慢，也不便于存儲，但是太小的e會導致安全性問題。所以限定1

(2)加密

輸入明文，根據公鑰(e，n)和公式C=Me(modn)可得密文。本文選擇要加密的明文為1234，由公式可得密文為2793。根據計算結果可知此加密算法加密所用的時間為2.667 ms。

(3)解密

輸入3調用第三個模塊來實現解密功能。RSA加密算法解密所需要的條件是知道密文和私鑰，根據M=Cd(modn)可得到明文。由計算得到密文為2793，私鑰為233，所以可解的密文為1234，從而實現了解密功能。

RSA加密算法的實現過程如圖2所示。

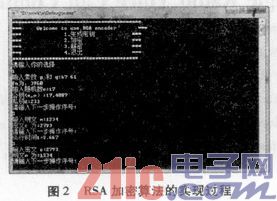
大整數因子分解問題向來被數學界視為世界性難題。正是基于這一點，RSA公鑰密碼體制才能夠以其較高的安全性為人們廣泛接受。但是RSA公鑰密碼體制也存在諸多不足之處：加解密算法中涉及大量的數值計算問題導致計算時間開銷較大，在一定程度上限制了其應用范圍。且密鑰的產生受到素數產生技術的限制，因而很難做到一次一密。為保證安全性必須選取1024 bits或以上，但這就使得運算速度較慢，而且隨著大數分解技術的發展，這個長度還在增加，不利于數據格式的標準化，致使其實現的難度增大，實用性降低。

因此，如何提高密鑰產生技術，發展更快速、更精確的大素數生成方法，完善RSA加密算法的大整數模冪乘運算，設計運算速度更快的求模和求冪算法，是很有意義的—個探索方向。

3 RSA加密算法的改進及實現

針對RSA加密算法加密速度慢的問題，經過進一步的研究，提出了SMM算法。SMM(Symmetry of Modulo Multiplication)算法是利用乘同余對稱特性來減少RSA加密計算中乘法和求模運算量的一種快速算法。RSA加密是對明文求冪剩余的過程為：

y=n (1)

傳統RSA算法是將指數表示成二進制數的形式，并將冪乘變成一系列乘同余的迭代。SMM算法是在每步迭代中對乘數進行有條件的代換。乘同余和平方剩余的對稱性有：

(n-i)(n-j)≡ijmod n (2)

(n-i)2mod n≡i2mod n (3)

j(n-j)≡(n-j)i≡-ijmod n (4)

其代換情況如下：如果ai-1表示第i-1步迭代的結果，則在進行第i步迭代時，若ai-1或g(n-1)/2，則保持原數不變;如果ai-1或g≥(n-1)/2則使用n-ai或n-g來代替ai-1或g[8,9]。

由于使用SMM方法，減少了乘法時間和求模運算量，改進后的RSA加密算法理論上可以使得算法速度得到一定程度的提高。

為了方便將改進前后的算法做比較，本文隨機素數p、q仍選擇61和67。根據f(n)=(p-1)(q-1)可得f(n)為3960 c，隨機數e選擇17，可得公鑰為(17，4087)，私鑰為233。改進后的RSA加密算法運行結果如圖3所示。與圖2對比可知，相同初始條件下原RSA算法所用的加密時間為2.667 ms，改進后算法所用的加密時間為1.669 ms，加密速度提高了約37.4%，且程序的復雜度也有所降低。

改進后的RSA加密算法可以通過簡單的循環迭代完成整個RSA加解密過程，減少了將十進制數據轉化為二進制數組和用擴展的歐幾里得算法求乘法逆元這兩步，不僅降低了程序的復雜性，而且提高了運算的效率。

4 結論

本文針對RSA加密算法時間開銷高和程序復雜的缺點，提出一種基于乘同余特性的SMM加密改進算法，該改進算法可減少RSA模冪乘運算過程耗時以及提高RSA加解密速度。最后通過改進前后算法的實例對比證明了本文所提改進RSA加密算法的有效性。