基于MRAS的永磁同步電機矢量控制系統仿真研究
摘要:基于MRAS的無速度傳感器矢量控制法把模型參考自適應法與轉速直接計算法結合了起來,設計了合適的自適應控制率,提高了轉速估計的精確度,在此基礎上,利用Matlab/Simulink構建MRAS無速度傳感器矢量控制系統仿真模型,仿真結果表明,轉速估計精度較高,系統具有一定的魯棒性。
本文引用地址:http://www.j9360.com/article/201610/306613.htm關鍵詞:永磁同步電機;模型參考自適應;無速度傳感器;Matlab/Simulink
在高性能的交流電機變頻調速系統中,不管是采用矢量控制還是直接轉矩控制,轉速的觀測和閉環控制環節是必不可少的。通常,采用光電碼盤等速度傳感器進行轉速檢測,并反饋轉速信號。但是,速度傳感器的安裝給系統帶來一些缺陷:
1)增加系統的成本,碼盤精度越高,價格越貴;
2)碼盤在電機軸上的安裝存在同心度問題,安裝不當將影響測速精度;
3)增加了電機軸向設備,給電機的維護帶來一定困難;
4)在惡劣的環境下無法工作,且碼盤工作精度易受環境條件的影響。
因此,越來越多的學者將目光投向了無速度傳感器控制系統的研究。現今已經有許多方法可以對電機轉速進行估計,主要有:基于電動機數學模型計算出轉速;利用感應電動勢和磁鏈計算速度;運用模型參考自適應原理來辨識速度;向電機注入高頻信號,利用電機的結構特征檢測出轉速等。模型參考自適應法(MRAS)就是其中使用頻率較高的一種方法。本文首先簡單分析了基于模型參考自適應法估計轉速的原理,并以此基礎在Matlab/Simulink中對轉速估計進行建模,最終搭建出基于MRAS的無速度傳感器矢量控制系統,并對其進行仿真驗證。
1 模型參考自適應法的原理
MRAS核心是模型參考自適應辨識,主要思想是將含有待估計參數的方程作為可調模型,將不含未知參數的方程作為參考模型,并且兩個模型具有相同物理意義的輸出量。兩個模型同時工作,利用輸出量之間的差值構成合適的自適應率,調節可調模型的參數,以達到控制對象輸出跟蹤參考模型的目的。
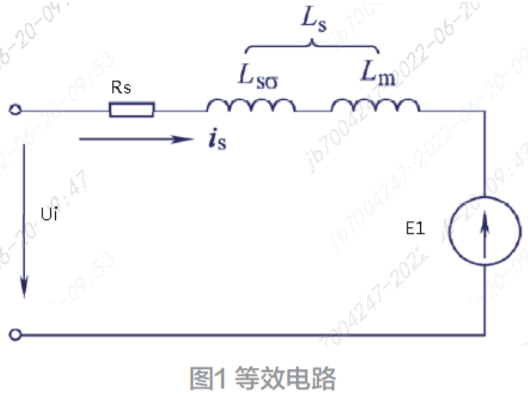
永磁同步電機在兩相旋轉(dq)坐標下的定子電流方程為:
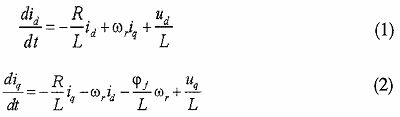
由式(1)、(2)可以看出,定子電流的數學模型只與電機的轉速wr有關,所以選擇電流模型作為可調模型,永磁同步電機本身作為參考模型,同時采用并聯型結構進行轉速辨識。為便于對系統的穩定性進行分析,應使轉速wr存在于系統的狀態矩陣中,對以上兩式中控制量與狀態量進行變化得:
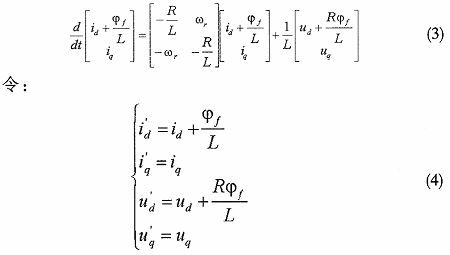


對Popov積分不等式進行逆向求解,即可得到自適應規律如式(9)所示。
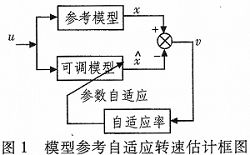
基于模型參考自適應法的電機轉速估計模型框圖如圖1所示。
在Matlab/Simulink環境下,按照上述方法建立的基于模型參考自適應的電機轉速估計仿真模型如圖2所示。
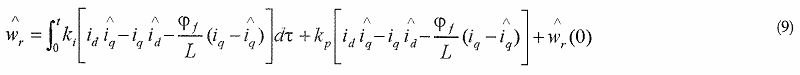

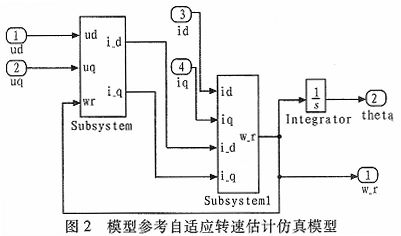
2 基于MRAS的永磁同步電機矢量控制系統仿真
通過上文的分析及建模,在Matlah/Simulink環境搭建基于模型參考自適應的速度估計的矢量控制系統,其中使用的永磁同步電機參數為:極對數P=4,定子電阻R=0.958 5 Ω,d軸和q軸電感Ld=Lq=5.25 mH,磁極磁通ψf=0.182 7 Wb,轉動慣量J=0.000 632 9kg·m2,功率器件的開關頻率是10 kHz。仿真結構如圖3所示。

主體部分采用的是基于電壓空間矢量PWM矢量控制系統,基于模型參考自適應的速度估計器代替了傳統轉速檢測的環節,搭建出了無速度傳感器矢量控制系統。
3 仿真結果
3. 1 轉速估計仿真結果
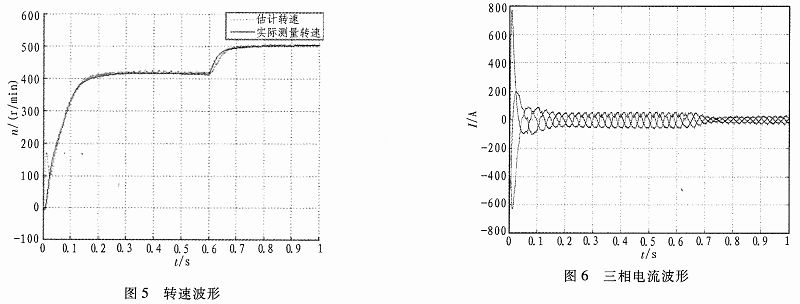
圖4為估計轉速和電機測量模塊輸出的實際轉速間的比較。設定總的仿真時間為1 s,速度給定500 r/min。
圖(a)中波形中有小幅波動的是估計轉速,圖(b)波形比較平滑的是輸出的實際轉速,總體來看差異很小。
3. 2 系統仿真結果
由圖3總仿真模型,通過仿真可得到基于模型參考自適應的速度估計矢量控制系統性能。其仿真結果圖如下所示。
轉速設定為50O r/min,系統加負載80 N·m啟動運行,在0.6 s時負載降為0。
圖5為電機轉速波形,虛線部分為估計轉速,實線部分為測量轉速,由圖可以看出估計轉速緊緊跟隨著測量轉速,由于帶負載運行,電機穩定時轉速略有下降,負載下降后,轉速最終穩定在500 r/min。
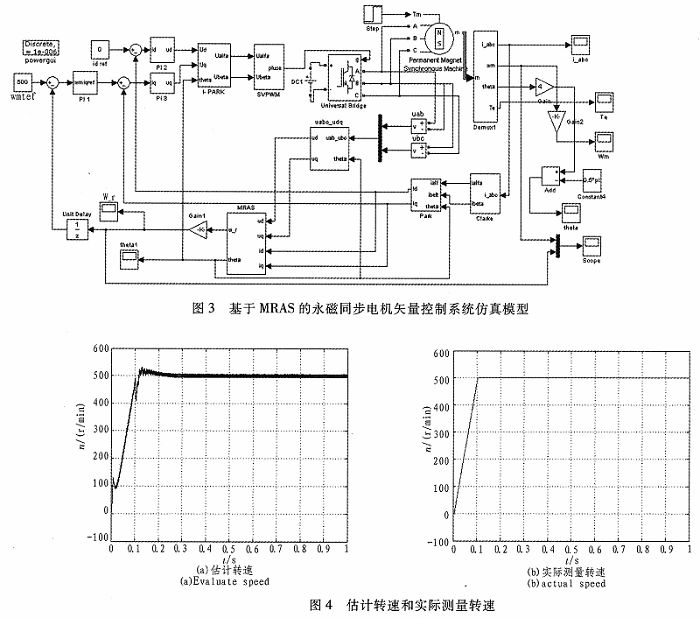
圖6為電機三相電流仿真波形,系統加負載啟動運行,越經過0.2 s電流波形穩定在50 A,在0.6 s負載降為0時,經過0.08 s左右的反應時間,電流穩定在30 A。
圖7為電機轉矩波形,因帶負載,啟動轉矩上升至350N·m左右,0.2 s后穩定在80 N·m,負載降為0后,轉矩也趨近于0 N·m。
4 結束語
由上述仿真結果可得,基于MRAS的轉速估計基本能夠估計出電機轉速,矢量控制系統完全省略了速度檢測環節,消除了速度傳感器的安裝帶來的誤差,簡化了系統的構成,而且結果顯示矢量控制系統具有一定的穩定性和可靠性,因此基于MRAS的速度估計將具有很好的研究價值。









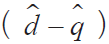

評論