近年來隨著基因芯片和DNA微陣列等高通量檢測技術的發展，產生了眾多的基因表達數據。對這些數據進行有效的分析已經成為后基因組時代的研究重點。一般的聚類是根據數據的全部屬性將數據聚類，這種聚類方式稱為傳統聚類。傳統聚類只能尋找全局信息，無法找到局部信息，而大量的生物學信息就隱藏在這些局部信息中。為了更好地在數據矩陣中搜索局部信息，人們提出雙聚類概念，目前這種聚類方法得到了越來越廣泛的應用。

本文對雙聚類提出以來的研究成果進行綜述。從基本思想、性能和雙聚類結果評價等角度總結重要的雙聚類算法類型。

1 雙聚類概念

自從基因芯片技術產生以來，大量的生物數據需要分析，這些數據大多規格化后以矩陣形式表示和存儲。基因芯片數據中隱藏了大量有用的局部模式，為尋找這些信息，CHENG and CHURCH于2000年提出了雙聚類(bicluster)概念[1]，并給出了雙聚類的定義：

定義1：設X為基因集，Y為對應的表達條件集。aij為基因表達數據矩陣A中的元素。設I、J分別為X、Y的子集，則(I，J)對指定的子矩陣AIJ具有以下平均平方殘基：

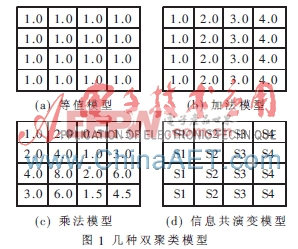
雙聚類的目的就是在基因表達數據矩陣中尋找滿足條件的子矩陣，使得子矩陣中基因集在對應的條件集上表達波動一致，反之亦然。不同的雙聚類算法采用不同的方式度量結果質量，所能找到的雙聚類類型是有很大差別的。目前較廣泛的模型有四種：矩陣等值模型、矩陣加法模型、矩陣乘法模型和信息共演變模型。圖1顯示了這幾種模型。

2 雙聚類算法分類

2.1 基于傳統聚類的雙聚類

這是一類最基本的雙聚類方法，以傳統聚類為雙聚類的基礎，基本思想是通過傳統聚類分別對矩陣的行和列進行聚類，然后合并聚類結果。具有代表性的是GETZ G等人[2]提出的耦合雙向聚類(Coupled two-way clustering)算法。算法開始于初始矩陣，創建兩個集合，一個只包含所有行，另一個只包含所有列。對這兩個集合分別運用分層聚類，以產生穩定的行和列的聚類，迭代上述聚類過程來尋找符合條件的穩定子集，將每次產生的穩定基因子集和條件子集分別加在各自的集合中，如此直到沒有新的穩定的雙聚類出現。基于傳統聚類的算法還有很多，如QU[3]等人采用模糊c均值來尋找相似子矩陣模型，通過分別對行和列應用傳統聚類得到中間結果，然后合并這些中間結果得到最終雙聚類。這類算法實現上較為容易，可以根據不同的需求選擇不同的傳統聚類算法，算法更加靈活。但這類算法無法完全脫離聚類的全局性，不能很好地尋找局部模式。為克服基于傳統聚類算法的缺陷，應該盡量避免傳統聚類的全局聚類的思想。如BHATTA A等[4]提出的BCCA算法就很好地避免了全局聚類，算法基于傳統聚類的一種距離度量方式，即pearson相關系數，通過計算刪除一些使person相關系數明顯增加的行列，從而得到雙聚類。但BCCA算法不能尋找波動一致而pearson距離較遠的雙聚類。

2.2 貪心迭代搜索

為擺脫傳統聚類的局限性和更好地提高效率，很多算法采用了貪心迭代搜索方法尋找雙聚類。CHENG and CHURCH首次使用這種方法尋找雙聚類，提出了著名的CC（CHENG and CHURCH）算法[1]。CC算法通過逐步刪除可以使子矩陣的平均平方殘基降低的行和列，得到一個最初的雙聚類，然后逐步添加不會使子矩陣平均平方殘基增加的行和列，得到一個較滿意的雙聚類。為找到更多雙聚類，算法使用隨機數覆蓋已經找到的雙聚類，再進行刪除和添加過程從而得到指定個數的雙聚類結果。算法能夠較快地得到用戶指定數目的雙聚類，但缺陷很明顯，隨機數替換會改變原始數據，造成結果的不精確，也無法找到重疊的雙聚類，而且容易陷入局部最優。YANG[5]等人對CC算法進行了改進，提出了FLOC算法。該算法首先生成一定數量的種子，然后通過計算添加或刪除某一行或列，每一步盡量使得雙聚類的中間結果增益改變最大。FLOC算法雖然可以找到可重疊的雙聚類，但雙聚類結果的好壞與運行時間都很大程度地依賴于初始聚類，而這些初始聚類往往都是隨機產生的。雙聚類的貪心策略效率較高，但聚類結果容易陷入局部最優。為克服貪心策略陷入局部最優的缺陷，一些算法首先采用貪心策略尋找雙聚類，然后對找到的雙聚類再應用智能優化算法以得到較理想的結果。如STEFAN等人[6]對CC算法進行了改進，即在添加刪除過程中好的行列有較大保留概率，反之較小，迭代得到的結果作為種子，應用進化算法優化產生較理想的雙聚類。

2.3 雙聚類窮舉策略

嚴格地說,采用窮舉方式尋找雙聚類是不現實的。原數據矩陣的子矩陣數量通常都異常龐大，所以采用窮舉策略尋找雙聚類算法，多數為窮舉小的子矩陣然后合并這些子矩陣的過程。WANG[7]等人提出的δ-Pcluster算法先找到所有基因對和條件對中滿足一定條件的雙聚類，然后根據條件對的聚類結果對基因對的聚類結果進行剪枝，以基因對條件上的聚類結果剪枝，得到較少的小雙聚類構建前綴樹，通過后序遍歷尋找雙聚類。δ-Pcluster算法只為加法模型定義了收斂函數，所以只能限制在加法模型的雙聚類上。LIU[8]等人改進了δ-Pcluster算法，采用多個閾值對應多種雙聚類模式，可以通過定義多種分組函數，構建了一個OPC樹將雙聚類的子結果添加入OPC樹，通過一次深度優先遍歷即可尋找到不同雙聚類模式。SAMBA算法[9]是另一個比較重要的基于窮舉的雙聚類算法，該算法使用統計模型將雙聚類問題轉化為一個完全平衡二分圖搜索問題，再尋找基因表達譜模式，即尋找具有波動一致性的子矩陣問題轉化為在二分圖中找稠密子圖問題。然而，這一算法的重要意義在于：對于基因表達譜進行雙聚類分析，實質上是一個NP-hard問題。所以，使用窮舉策略的雙聚類算法雖然能夠找到較優的雙聚類，但算法的時間復雜度會隨矩陣規模的增大而呈指數增長。因此必須限制雙聚類矩陣的大小，同時利用算法技巧優化窮舉過程，才能保證算法的效率。

2.4 數學模型方法

利用數學中較成熟的理論或通過建立模型尋找雙聚類，一直是研究的熱點，也是近年來雙聚類發展中的一個趨勢。由于雙聚類問題的特殊性，即在矩陣中尋找有規律的子矩陣，所以可以較容易地轉換成數學模型問題。這類算法中較重要的有LAURA[10]提出的格子模型（Gibbs sampling），它將整個數據集建模為基于聚類表達模式的疊加。也就是說，假如一個突出值屬于多個簇，則它等價于這些簇的所有背景值、行影響、列影響的疊加。格子模型更適合確定那些重疊簇，但是這個模型所使用的貪心算法的固有性質卻阻礙了這一目標的實現。假設某一值是由多個簇疊加產生的，當確定第一個簇時，實際上這個值受到了所有疊加簇的影響，這意味著這個值將極大地偏離第一個簇的模型。這將導致它被排除到簇外，而實際上它本來是應該在這個簇內的。GU等[11]在Gibbs sampling的基礎上提出了貝葉斯雙聚類模型(BBC)，這種是完全基于模型的一種方法，所以不需要任何閾值參數就能尋找到重疊的雙聚類。Kluger[12]等提出的Spectral Biclustering應用線性代數技術尋找數據中的雙聚類結構，將在一個條件集上波動一致的基因集看做一種隱藏的棋盤模式，使用特征向量計算尋找這種模式。這類算法的共同之處在于將雙聚類問題轉化成數學或其他模型，應用各種方法尋找這些模型。數學模型方法尋找雙聚類的缺陷也很明顯，就是一種數學模型只對應一種或少數的雙聚類類型。表1是對以上四種類型優缺點的總結。

2.5 其他雙聚類方法

另外的一些較重要方法還有采用分治策略尋找雙聚類。其思想是，先將矩陣劃分成若干子矩陣，然后對子矩陣進行雙聚類，最后合并小的聚類而得到最終結果。這類算法的優點是執行速度較快，但是缺點是算法可能錯過一些好的雙聚類，因為在發現它們之前，這些雙聚類可能己經被分割。模仿生物現象或自然的進化算法越來越普遍，這些方法在數據挖掘和雙聚類中有著廣泛的應用。如DIVINA等[13]將多目標進化算法應用于雙聚類，同時優化多個目標，來發現全局最優解。BRYAN等[14]應用模擬退火模型尋找雙聚類，都得到了較好的效果。

3 雙聚類結果度量

目前雙聚類實驗公認的兩個數據集分別是：啤酒酵母細胞周期表達值[15]和人類B細胞表達值[16]。雙聚類結果質量評價標準有可視化和非可視化標準。雙聚類的可視化主要有通過明暗度觀察矩陣結構的熱圖、通過點線連接觀察波動性的坐標圖、通過基因節點的帶有方向性的連接的表達譜圖。BARKOW等人[17]開發了一個著名的雙聚類算法平臺，使用其中的熱度圖可以較直觀地看到數據矩陣的規模，通過明暗度大致了解基因表達的強度。其中也實現了坐標圖，這是目前廣泛使用的雙聚類可視化方式，可直觀地看到基因曲線波動的一致性。

非可視化標準往往結合可視化共同度量雙聚類算法或雙聚類結果的好壞。不同的雙聚類策略在時間花費上相差很大，又由于雙聚類是NP-hard問題，所以運行時間是度量雙聚類算法好壞的一個重要因素。至于雙聚類個體的質量，往往會看它是否接近四種基本模型。平均平方殘基H是度量結果是否接近模型的較好方式，也是現階段通常采用的度量手段。雙聚類的大小S即包含元素個數也是判斷雙聚類質量的標準，所以有了許多H的演變形式，例如H/S的形式可有效度量結果，其值越小聚類結果越好。在整個矩陣上找到多個雙聚類，所以覆蓋矩陣元素的全面性和雙聚類結果的重疊性也是重要的質量評價標準。能否找到可重疊的雙聚類是設計雙聚類算法要考慮的，而結果是否能有效地覆蓋矩陣中所有元素也是重要的。另外還有其他的雙聚類度量方式，例如在同一雙聚類結果上發現了更多屬于這個雙聚類的基因，而這些基因沒有被其他方法發現。

雙聚類是個較為年輕的研究領域，近十幾年的研究提出了很多有效算法，應用這些算法分析生物芯片數據的過程中也發現了許多有意義的生物學結果。如今雙聚類領域雖然主要應用于基因表達數據，但隨著研究的發展也將會應用于電子商務等多種領域。由于雙聚類問題本身的復雜性，今后依然是個有挑戰性的研究課題。

參考文獻

[1] CHENG Y, CHURCH G M. Biclustering of expression data[C]. Proc. Eighth Int’l Conf. Intelligent Systems for Molecular Biology (ISMB’00), 2000:93-103.

[2] GETZ G, LEVINE E, DOMANY E. Coupled two-way clustering analysis of gene microarray data[C]. In Proceed ings of the Natural Academy of Sciences USA, 2000:12079-12084.

[3] Qu Jinbin, MICHAEL N, Chen Luonan. Constrained subspace clustering for time series gene expression data[C]. In 4th International Conference on Computational Systems Biology, 2010:9-11.

[4] BHATTACHARYA A, DE R K. Bi-correlation clustering algorithm for determining a set of co-regulated genes[J]. Bioinformatics, 2009, 25(21): 2795-2801.

[5] Yang Jiong, Wang Wei. Enhanced biclustering on gene expression data[C]. In Proceedings of the 3rd IEEE Conference on Bioinformatics and Bioengineering, 2003:321-327.

[6] BLEULER S, PRELIC A, ZITZLER E. An EA framwork for biclustering of gene expression data[C]. Evolutionary Computation, 2004:166-173.

[7] Wang Haixun, Wang Wei, Yang Jiong, et al. Clustering by pattern similarity in large data sets[C]. Proc. The ACM SIGMOD International Conference on Management of Data, 2002:394-405.

[8] Liu Jinze, Wang Wei. Op-cluster: clustering by tendency in high dimensional space[C]. In Proceedings of the 3rd IEEE International Conference on Data Mining, 2003:19-22.

[9] TANAY A, SHARAN R, et al. Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data[C]. ProcNatl Acad Sic U S A.,2004: 2981-6.

[10] LAZZERONI L, QWEN A. Plaid models for gene expression data[J]. Statistica Sinica, 2002 (12):61-86.

[11] Gu Jiajun, LEE J S. Bayesian biclustering of gene expression data[C]. International Conference on Bioinformatics and Computational Biology, 2007: 25-28.

[12] KLUGER Y, BASRI R, ChANG J T, et al. Spectral biclustering of microarray data：coclustering genes and conditions[J]. Genome Res, 2003,13(4):703-16.

[13] DIVINA F, AGUILAR,RUIZ J S. A multi-objective approach to discover biclusters in microarray data[C]. Proceedings of the 9th annual conference on Genetic and evolutionary computation, 2007: 385-392.

[14] BRYAN K, CUNNINGHAM P, BOLSHAKOVA N. Biclustering of Expression Data Using Simulated Annealing[C].18th IEEE Symposium, 2005: 383-388.

[15] CHO R J, CAMPBELL M J, WINZELER E A, et al. A genome-wide transcriptional analysis of the mitotic cell cycle[J]. Molecular Cell, 1998, 2(1): 65-73.

[16] ALIZADEH A A, Eisen M B, Davis R E, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling[J]. Nature, 2000(403):503-511.

[17] BARKOW S, BLEULER S, PRELIC A, et al. BicAT:biclustering analysis toolbox[J]. Bioinformatics, 2006,22(10):1282-1283.

更多醫療電子信息請關注：21ic醫療電子頻道