邊緣檢測算法在醫學超聲液性病變圖像中的應用
1.1.3 Prewitt算子
Prewitt和Sobel算子都是使用3×3模板的一階微分算子,它們是在研究曲面擬合的基礎上提出的。擬合是指已知某連續函數的一系列離散函數值,通過最小二乘法等準則來確定該函數中的待定系數。Prewitt和Sobel算子的2個差分模板的系數之間的區別僅在于求平均的方法不同。隨后出現的Kirseh算子用不等權的8個3×3循環平均梯度算子分別與圖像進行卷積,取其中的最大值輸出,它可以檢測各個方向上的邊緣,減少了由于平均而造成的細節丟失,但同時增加了計算量。
1.2 基于二階微分的邊緣檢測算法
前面討論了基于一階微分的邊緣檢測,如果所求的一階微分高于某一閾值,則確定該點為邊緣點。一階微分組成的梯度是一種矢量,不但有大小還有方向,和標量比較,數據存儲量比較大。一種更好的方法就是求梯度局部最大值對應的點,并認定它們是邊緣點,通過去除一階微分中的非局部最大值,可以檢測出更精確的邊緣。一階微分的局部最大值對應著二階微分的零交叉點,這意味著在邊緣點處有一階微分的峰值,同樣地,有二階微分的零交叉點。這樣,通過找圖像強度的二階微分的零交叉點就能找到邊緣點。
在二維空間,對應二階微分有兩種算子:Laplace算子和Marr算子。Laplace算子也稱拉氏算子,它的特點是具有旋轉對稱性而不具備方向性,只需要一個3×3模板。Laplaee算子是對二維函數進行運算的二階導數算子,與方向無關,對取向不敏感,因而計算量要小。根據邊緣的特性,Laplace算子可以作為邊緣提取算子,計算數字圖像的Laplaee值可以借助模板實現,但是它對噪聲相當敏感,它相當于高通濾波,常會出現一些虛假邊緣。由于Laplace算子存在著諸多缺陷,它一般并不直接應用于邊緣檢測,而是結合其它方法以提高邊緣的定位精度。而Marr算子就是在Laplace算子基礎上改進,由于它使用的是高斯型的Laplace模板,因此又被稱作LOG算子,先對圖像用Gauss函數進行平滑,然后利用Laplace算子對平滑的圖像求二階導數后得到的零交叉點作為待選邊緣。LOG算子就是對圖像進行濾波和微分的過程,是利用旋轉對稱的LOG模板與圖像做卷積,確定濾波器輸出的零交叉位置。
1.3 Canny算子
Canny算子是最常用的邊緣檢測方法之一,是一個具有濾波、增強和檢測的多階段的優化算子。
該算法的基本過程如圖1所示。本文引用地址:http://www.j9360.com/article/193780.htm
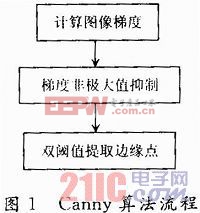
Canny算子檢測邊緣的實質是求信號函數的極大值問題來判定圖像邊緣像素點。基本步驟為:
(1)用高斯濾波器平滑圖像;
(2)用一階偏導的有限差分來計算梯度的幅值和方向;
(3)對梯度幅值進行非極大值抑制;
(4)用雙閾值算法檢測和連接邊緣。Canny算子能夠得到連續完整的圖像,但需要注意的問題是:Gauss濾波的尺度,以及雙閾值的選擇。
1.4 基于Snake模型的邊緣檢測算法
Snake模型是1987年由Kass提出的,它的基本思想是以構成一定形狀的控制曲線為模板(或者稱為輪廓線),通過模板自身的彈性形變與圖像局部特征相匹配達到調和,即某種能量函數極小化,完成對圖像邊緣的提取,通過對模板的進一步分析而實現圖像的理解和識別。能量最小化模型已經有了很長的發展歷史,Kass對其進行了改進,采用動態調整的方法來實現它,對圖像的高層信息進行分析和提取而不至于受到太多低層信息的影響。通過在原始的最小化函數中加入外力因子,可以引導初始化的輪廓線朝著特定的方向前進,最后達到提取目標邊界的目的。
1.4.1 基本Snake模型
Kass等提出的基本Snake模型由一組控制點組成,即v(s)=(x(s),y(s)),s∈[0,1],其中x(s)和y(s)分別表示每個控制點在圖像中的坐標位置,s是以傅立葉變換形式描述邊界的自變量。其對應的能量函數定義為:
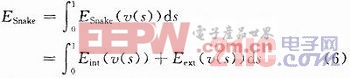
式中:Eint為曲線的內部能量;Eext為外部能量。
內部能量定義為:
![]()
式中|vs(s)|為彈性能量,是曲線相對于弧長的一階導數的模,受彈性系數的調節,控制著曲線的張力。|vss(s)|是彎曲能量,是曲線相對于弧長的二階導數的模,受剛性系數的調節,控制曲線的變形程度。
對于普通的灰度圖像I(x,y),典型的外部能量(外部力)表達有如下2種定義:
![]()
式中為梯度算子,是方差為σ的二維高斯函數。在圖像邊緣區域,圖像灰度值的梯度往往較大,取反后計算以滿足能量最小的要求。




評論