摘　要: 采用Verilog HDL語言, 在FPGA上實現了32位單精度浮點乘法器的設計, 通過采用改進型Booth編碼，和Wallace 樹結構, 提高了乘法器的速度。本文使用Altera Quartus II 4.1仿真軟件, 采用的器件是EPF10K100EQ 240 -1, 對乘法器進行了波形仿真, 并采用0.5CMOS工藝進行邏輯綜合。
關鍵詞: 浮點乘法器; Boo th 算法; W allace 樹; 波形仿真

隨著計算機和信息技術的快速發展, 人們對微處理器的性能要求越來越高。乘法器完成一次乘法操作的周期基本上決定了微處理器的主頻, 因此高性能的乘法器是現代微處理器中的重要部件。本文介紹了32 位浮點陣列乘法器的設計, 采用了改進的Booth 編碼, 和Wallace樹結構, 在減少部分積的同時, 使系統具有高速度, 低功耗的特點, 并且結構規則, 易于VLSI的實現。

1　乘法計算公式

32 位乘法器的邏輯設計可分為: Booth編碼與部分積的產生, 保留進位加法器的邏輯, 乘法陣列的結構。

1.1　Booth編碼與部分積的邏輯設計
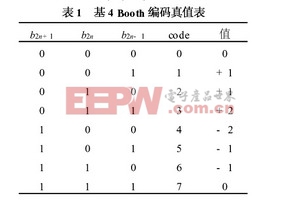
尾數的乘法部分,本文采用的是基4 Booth編碼方式, 如表1。首先規定A_m和B_m表示數據A和B的實際尾數,P 表示尾數的乘積, PP_n表示尾數的部分積。浮點32 位數, 尾數是帶隱含位1 的規格化數, 即: A_m =1a₂₂a_21….a₀和B_m = 1 b₂₂b₂₁.…b₀, 由于尾數全由原碼表示,相當于無符號數相乘, 24 24 位尾數乘積P 的公式為:





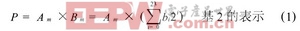
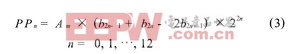
1.2　乘法器的陣列結構
本文采用的是3 -2 加法器, 輸入3 個1 位數據: a, b,ci; 輸出2 個1 位數據: s, Co。運算式如下:

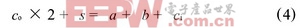
其邏輯表達式如下:


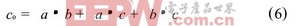
當每個部分積PP_n 產生之后, 將他們相加便得到每個乘法操作的結果。相加的步驟有很多, 可采用的結構和加法器的種類也很多。比如串行累加:


而Wallace 樹的乘法陣列如下:


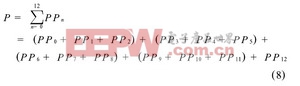
加法器之間的連接關系如圖1, 圖2 所示, 或者從公式(7) 與(8) 中可以看出, 圖1中串行累加的方法延遲為11個3-2 加法器的延遲, 而圖2中, Wallace樹延遲為5個3 -2加法器的延遲。圖1的延遲比圖2的延遲大。

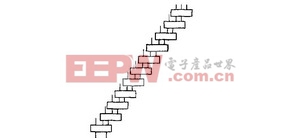
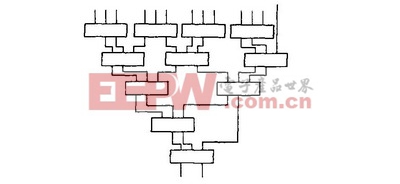
圖1　串行累加 圖2　Wallace 樹

2　32 位浮點乘法器的設計

本文是針對IEEE754 單精度浮點數據格式進行的浮點乘法器設計。IEEE754 單精度浮點格為32位, 如圖3 所示。設A ,B均為單精度IEEE754格式, 他們的符號位, 有效數的偏移碼和尾數部分分別用S , E 和M來表示。雙精度和單精度采用的運算規則是一致的, 只是雙精度的位長增加了一倍, 雙精度是64位, 其中尾數52位, 指數11位, 1位符號位。所以提高了精度范圍。

圖3　32 位浮點數據格式

32 位浮點數據格式: A = (- 1) ^S M 2^E-127。其中乘法器運算操作分4步進行。
(1) 確定結果的符號, 對A 和B 的符號位做異或操作。
(2) 計算階碼, 兩數相乘, 結果的階碼是兩數的階碼相加, 由于A 和B 都是偏移碼, 因此需要從中減去偏移碼值127,得到A 和B 的實際階碼, 然后相加, 得到的是結果的階碼, 再把他加上127, 變成偏移碼。
(3) 尾數相乘,A 和B 的實際尾數分別為24位數, 即1M_a 和1M_b, 最高位1是隱藏位, 浮點數據格式只顯示后23位, 所以尾數相乘結果應為一個48位的數據。
(4) 尾數規格化, 需要把尾數相乘的48位結果數據變成24 位的數據, 分3步進行:

① 如果乘積的整數位為01, 則尾數已經是規格化了;如果乘積的整數位為10, 11, 則需要把尾數右移1位, 同時把結果階碼加1。
② 對尾數進行舍入操作, 使尾數為24位, 包括整數的隱藏位。
③ 把結果數據處理為32位符合IEEE浮點數標準的結果。包括1位符號位, 8位結果階碼位, 結果23尾數位。

3　32 位浮點乘法器的實現與仿真

圖4 列出本設計的FPGA 仿真結果。圖中data1是被乘數, data2是乘數, reset是清零信號, 高有效。start 是開始信號, 也是高有效。dataout10是兩個浮點32 位數相乘, 進行規格化以后的結果, 是一個32 位數。Product 是24位尾數相乘的結果, 是一個48位數。

圖4　32 位浮點乘法器的仿真結果
整個設計采用了VHDL和Verilog HDL語言進行結構描述, 如果采用的是上華0.5 的標準單元庫, 并用Synopsys DC 進行邏輯綜合, 其結果是完成一次32位浮點乘法的時間為30ns, 如果采用全定制進行后端版圖布局布線, 乘法器性能將更加優越。

4　結　語

本文給出了32 位浮點乘法器的設計, 浮點算法具有高精度性以及較寬的運算范圍, 使得乘法的設計更能夠滿足工程和科學計算的要求, 電路的設計、模擬和實現均采用Altera Quartus II 4.1開發工具。采用的器件EPF10K100EQ 240-1, 邏輯單元是1914個, PIN的數量是147,本設計采用了一系列的算法和結構, 如采用Booth編碼的方法和Wallace樹的結構, 使得系統具有高速度特點, 并且易于ASIC的后端版圖實現。