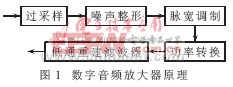
一般來說，高階Σ-Δ調制器比低階Σ-Δ調制器具有更好的性能。但大于二階的不能用線性模型描述，因為比較器的平均增益減小，使系統的穩定性下降。多級噪聲模型是解決穩定性較好的方案。該技術采用了多個級聯、穩定的一階回路，每階回路對上一級的積分器輸出與數模轉換器（DAC）輸出之差（量化噪聲）進行量化，最后差分求和輸出，它能夠使量化噪聲得到很好的抑制。多位結構的Σ-Δ調制器則可提高轉換速率和精度。對于一個給定的過采樣比和濾波器的階數，這種結構可以提供更大的動態范圍。多位調制器每增加1位，信噪比就能增加6dB，而且它還可以減少帶外的噪聲水平，降低對后級模擬濾波器的要求。但多位調制器的一個主要缺點是：由于在多位DAC中的元素不匹配而造成的積分非線性化問題，使每級的非線性化誤差得不到消除而逐漸累加而造成輸出結果惡化。本文提出了一種方法：在傳統的MASH結構基礎上，每級之間加一條反饋回路[3]。該方法能有效地消除多位DAC非線性化而帶來的誤差。
1 調制器原理
　　L階Σ-Δ調制器如圖2所示。Σ-Δ調制器的階數就是調制器前向通道積分器的個數。從圖中可以看出，L階Σ-Δ調制器的前向通道包括L個積分器和嵌于反饋回路的量化器，每個積分器的輸入均為前一個積分器的輸出與1位DAC的輸出之差。反饋回路的作用使得第一級積分器的凈輸入趨于零，即DAC的輸出與調制器的輸入信號X(n)基本相等，亦即X(n)≈Y(n)。

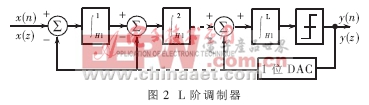
　　由于量化器為非線性元件，為了分析它所引入的量化誤差，需將量化器近似等效成一個相加性的白噪聲源e(n)，因此根據線性化系統疊加原理，得到調制器對信號和噪聲的傳輸函數如下：

　　從以上公式可以看出，增加階數、位數和過采樣率都可以讓調制器的信噪比和動態范圍有不同程度的提高。但隨著它們的提高，也會帶來負面影響。在過采樣率一定的情況下，增加位數能夠彌補階數變高而引起的動態范圍減小的問題，信噪比也會提高，但它引入的非線性誤差卻會使結果惡化。在減小多位系統中的DAC非線性化問題方面，人們提出了很多解決辦法，包括引入新的結構、校準技術、動態元素匹配技術（DEM）、雙端量化結構等[4]。在上述的方法中，動態元素匹配技術在解決多位系統中的非線性化問題中是應用最廣的。它通過計算出不匹配單元造成的誤差，從而得到一個修正算法，通常用得較多的算法有元素隨機化和元素旋轉等。但DEM的缺陷是強烈依靠它所使用的算法。例如DEM廣泛使用的DWA數據權重平均算法雖然能夠對第一階的噪聲進行整形，但是它也引入了信號依賴誤差而降低了動態范圍，雖然改進的雙向DWA算法能夠降低信號依賴誤差，但是使帶內的噪聲同時也增加了。因此，DEM大體上只是用在一階噪聲整形上[5]。為此本文提出了一種沒有采用DEM的4階級聯調制器的新方案，它在解決非線性化的問題上取得了較好的效果。