基于盒式圖的數據過濾與回歸分析算法
1 盒形圖和回歸分析簡介
1.1 盒形圖
該方法可以描述數據集取值范圍的情況,展示數據主要聚集的區域,發現離群數據可能的位置,以便于對離群數據進行處理。盒形圖顯示一個變量的信息,如對相同CMM等級的不同項目完成每個FP的工作量分析,根據中位數m、上四分位數u、下四分位數l、盒長d、和尾(tail)來分析。
中位數是在數據集中排列居中的項。也就是說,如果中位數取值為m,則數據集中有一半的值大于m,一半的值小于m。將所有數值按大小順序排列并分成四等份,處于三個分割點位置的得分就是四分位數。最小的四分位數稱為下四分位數l,所有數值中,有四分之一小于下四分位數,四分之三大于下四分位數。中點位置的四分位數就是中位數。最大的四分位數稱為上四分位數u,所有數值中,有四分之三小于上四分位數,四分之一大于上四分位數。也有叫第25百分位數、第75百分位數的。將上四分位數和下四分位數的距離定義為盒長d,因此,d=u-l。接下來定義分布的尾(tail)。理論上,上尾值點為u+1.5d,下尾值為u-1.5d,這些值必須進行舍位處理,以接近真實數據,位于上尾和下尾之外的值稱為離群值。
1.2 回歸分析方法
回歸分析方法是研究要素之間具體數量關系的強有力的工具,運用這種方法能夠建立反映要素之間具體的數量關系的數學模型,即回歸模型。線性回歸技術的基礎就是散點圖。將每個屬性對表示為一個數據點(x,y),然后用回歸技術計算出能夠最好地擬合這些點的直線。目標是將屬性y(因變量)根據屬性x(自變量)表示為等式:y=a+bx。
線性回歸的理論是從每個點垂直向上或向下畫一條線段到趨勢直線,表示從數據點到趨勢直線的垂直距離。在某種意義上,這些線段的長度表示數據和直線的差異,且這種差異應盡可能地小。因此,“最佳擬合”的直線式是指使該距離最小的直線。
在數學上要計算“最佳擬合”直線的斜率b和截距a是很簡單的。每個點的差異稱為殘差,生成線性回歸直線的公式是殘差的平方和達到最小。可以將每個數據點的殘差表示為:

2 算法實現
在進行數據清洗時,由于數據是無序輸入的,所以先對其排序,再用盒形圖法行數據清洗。以下是偽代碼:
void BubbleSort(double m,double q,int n) //先對輸入
//的數據進行冒泡排序,并相應修改
//第二組數據的順序,以保證它們之間的對應關系
{ for(int i=0;in;i++)
for(int j=n-1;j>i;j--)
{
輸入數據的排序
修改第二組數據
}
}
void box(double *m,double *q,int n) //盒形法篩選
//掉離群項目工作量數據,n為輸入數據個數,m、q為指針
{
double a,b,c,top,bottom,l; //上分位a,中位數b,//下分位c
if(n%2==0) //計算出3個四分位數
{
b=(*(m+n/2)+*(m+n/2-1))/2; //數據個數為
//偶數時,中位數取中間兩數的平均值
a=*(m+n/4);
c=*(m+3*n/4); }
}
else
{ b=*(m+n/2);
a=*(m+n/4);
c=*(m+3*n/4); }
l=c-a; top=c+1.5*l;bottom=c-1.5*l; //計算出盒
//長,上尾數,下尾數
if(bottom0) bottom=m; //并進行必要的舍位處理
int j=n;
for(int i=0;ij;i++) //判斷是否為離群值,
{
if(*(m+i)>top‖*(m+i)bottom)
如有,將其從數組中剔去
}
}



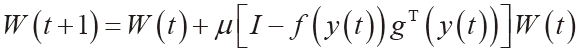

評論