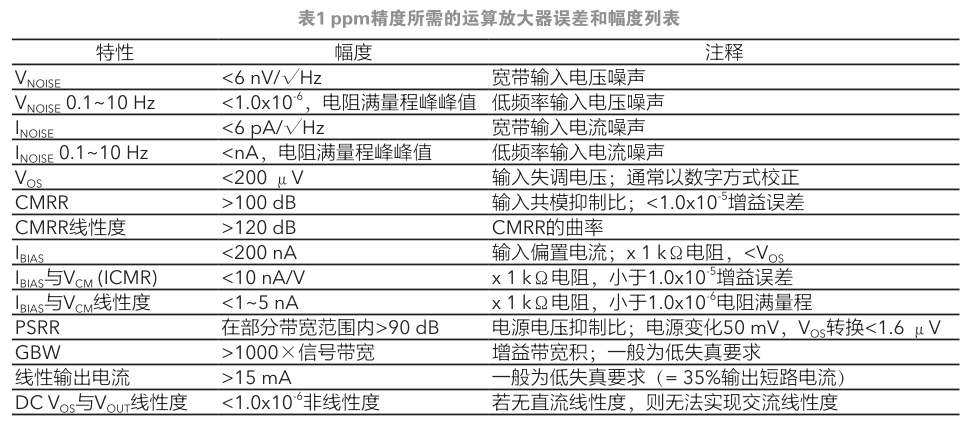
多級低通有源濾波器的設計考慮因素
概要
本文引用地址:http://www.j9360.com/article/187751.htm常見的多級低通有源濾波器的增益排序方法是把大部分乃至全部增益放在第一級。如果只考慮要降低低頻的輸入參考噪聲,這是正確的設計方法。然而,其它的幾種考慮因素可能會使您改變這種增益排序,以實現更為出色的實施方案。這些需要考慮因素包括:每級特征頻率范圍內的噪聲峰值效應、高 Q 值高增益級的過沖導致壓擺范圍受限和/或削波、可靠實施所需的放大器帶寬。本文將對上述情況進行描述,為其找出相應實施方案,并對這些方案的效果進行詳解。
每個多級有源濾波器設計人員都不得不為各級 Q 值的排序和每級該分配多少增益之間的折衷而大傷腦筋。如果濾波器的總增益要大于 1,最簡單的設計方法就是把大部分乃至全部的增益放在第一級。經過正確分析得出這種方法可以實現最低輸入參考點噪聲(當噪聲頻率遠低于濾波器特性頻率時)。另外,對于標準的多極點設計,需要從低到高布置一系列的 Q 值。在哪里布置 Q 值最高的一級是一個非常重要的考慮因素,實際上也是實施方案成功與否的關鍵。這些 Q 值最高的一級會出現最高的輸出噪聲峰值,也是最有可能導致壓擺范圍受限和/或者削波的階躍響應過沖的地方。許多設計工具把這一級放在最前面,這恰與將大多數增益放在第一級的目標相沖突。有些設計工具則把大多數增益放在最后一級,結果導致噪聲峰值遠遠超過必要水平,增大了濾波器輸出的整體噪聲。某些設計工具則采用折中方法,把 Q 值最高的一級放在中間(針對 4 階以上而言),這種方法似乎非常適用于某些應用。
在采用有自身性能限制的真實部件來真正構建這些濾波器時,上述的考慮就不再是紙上談兵。使用一種近期開發的在線設計工具(參考資料 1),可以開發出多種能夠實現相同目標頻率響應的案例。在選擇不同的增益和 Q 值排序的情況下,它們的階躍響應、噪聲以及要求的放大器性能裕量會大相徑庭。
當然,只有在設計的低頻通帶總增益大于 1 的情況下才需要考慮增益排序。盡管增益和 Q 值排序問題也適用于多級反饋 (MFB) 或無窮大增益拓撲,這里將使用 Sallen Key 濾波器 (SKF) 來說明問題和結果。有資料顯示特定 SKF 級實現的增益是受限的(參考資料 2)。這只在阻容解決方案受到某些其它限制時才會出現。一般假設需要等電容設計,實際上這將限制每級可實現的最小增益。然而,對于板級實施方案來說,等電容假設是人為的,可能對于針對集成的設計流程更有用處。這里的設計不局限于等阻或是等容,讓設計可以實現通帶內任何需要的增益。不過,需要注意的是,隨著增益的增加,這會加劇濾波器對組件變化和增益變化的靈敏度。一級增益的增加要求該級用于設置濾波器和增益的阻容元件具有更小的阻容容差。當然現在已經可以提供這樣的元件。
參考資料 1 的設計流程傾向于增大電阻,讓電阻產生的噪聲與運算放大器固有噪聲相比可忽略不計。同時設置 1/R2C2 極點,使之降低濾波器級的內部噪聲增益峰值(圖 1)
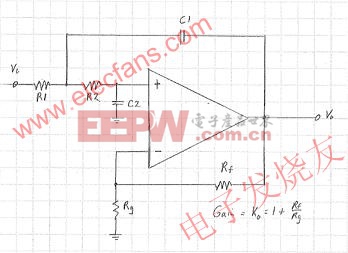
圖1. 基本的 SKF 二階低通濾波器
在各級增益分配中對要求的運算放大器帶寬的考慮
圖 1 所示的設計要成功實施,必須估算出最低的放大器閉環帶寬。通常,如果要求放大器帶寬乘數是目標 Fo 的 100 倍到 200 倍,就比較容易實現。更為復雜的設計會根據該級增益和目標 Q 值來計算目標帶寬,從而得到放大器帶寬隨 Fo 和 Q 值變化而變化的理想靈敏度。
帶寬乘數計算隨 Q 值變化(在給定增益下)的示例見圖 2。該圖顯示的是圖 1 電路的放大器帶寬與 Fo 之比,其目的是提供恰好足夠的放大器帶寬,實現高精度的濾波器實施方案,從而在帶寬變化為 15% 的情況下,Fo 變化不超過 2%(參考資料 3)。使用帶寬裕量高于本設計的放大器當然是可以的,不過本設計的目的是降低成功設計的門檻。

圖 2. 所需的運算放大器帶寬與增益和 Q 值的關系
要注意的是,本圖重點強調帶寬。這樣可以使用電流反饋放大器 (CFA) 或電壓反饋放大器 (VFA) 器件來實現 SKF 拓撲。CFA 器件在一定的增益范圍內,能夠保持恒定的閉環帶寬,故特別適合用于實現高增益。本圖(根據參考資料 1 的算法得出)在這個方面表現得特別明顯。舉例來說,在增益為 2,Q 值為 0.5 的情況下,它只需要 7 倍的帶寬裕量。在 25 倍帶寬裕量下,增益可以達到10,Q 值達到 4.5。這些相對適度的設計裕量允許使用更多種類的物理器件來實現特定的濾波器標準,但需要使用某些支持該帶寬的可以調整組件的算法,才能達成濾波器的設計標準。采用理想等式來計算阻容值的設計流程需要放大器帶寬具有更大的裕量。
若使用 VFA 器件,需要進行如下修正:將每個數據點與增益相乘,得到所需的增益帶寬積與 Fo 的比例。如圖 3所示,所有的曲線都上移并展開。
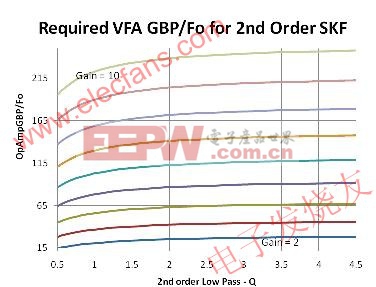
圖 3. 給定增益條件下所需的帶寬增益積與 Q 值參數






評論