變形耦合發電機混沌系統的追蹤控制
摘 要:針對變形耦合發電機混沌系統的結構特點,設計統一形式的非線性追蹤控制器。根據非線性系統的線性化穩定理論,對系統同步誤差穩定性進行分析和證明。這里所設計的控制器可以實現變形耦合發電機系統的狀態變量與任意給定參考信號的廣義同步。以追蹤常值信號、周期信號和混沌信號為例,進行數值仿真,進一步表明該控制方法的有效性。
關鍵詞:變形耦合發電機;追蹤控制;廣義同步;非線性控制器
0 引 言
混沌系統的控制和同步是當前自然科學基礎研究的熱門課題,它在通信、信息科學、醫學、生物、工程等領域得到了廣泛的應用,各種控制和同步方法也應運而生。在混沌控制研究中,追蹤問題是研究的一個熱點。追蹤問題即通過施加控制使受控系統的輸出信號達到事先給定的參考信號,更具有一般性。特別是,如果追蹤的參考信號是由混沌系統產生的,這種追蹤控制便演化成為驅動系統和響應系統的同步,它包括自同步和異結構同步,這方面的工作已經有了許多研究。電網之間的互聯是現代電力系統發展的必然趨勢,它將使電網的發電和輸電變得更經濟、更高效。與此同時,電力系統運行的穩定性受到前所未有的挑戰。隨著分岔、混沌理論在電力系統非線性動力學行為研究中的應用,人們發現電力系統中除了低頻振蕩外,還存在混沌振蕩。這種振蕩不僅對系統的穩定具有極強的破壞力,而且不能依靠附加傳統的勵磁控制器來抑制或消除。自20世紀90年代以來,國內外許多研究人員對電力系統的分岔、混沌振蕩產生機理進行了充分、有益的探討,但對電力系統混沌控制方法的研究尚屬少見。在此針對變形耦合發電機昆沌系統的結構特點,并基于非線性系統的線性化穩定理論,設計了一個統一形式的非線性追蹤控制器,可以實現變形耦合發電機系統的狀態變量與任意給定參考信號的廣義同步。該控制器簡單、易于實現。
l 系統模型
耦合發電機系統由一個具有混沌特征的三維自治方程組來描述,它是由連接在一起的2臺發電機組成,其中任何一臺發電機都處于另一臺發電機產生的電流所形成的磁場之中。文獻在基于耦合發電機系統的基礎上,給出了變形耦合發電機系統:

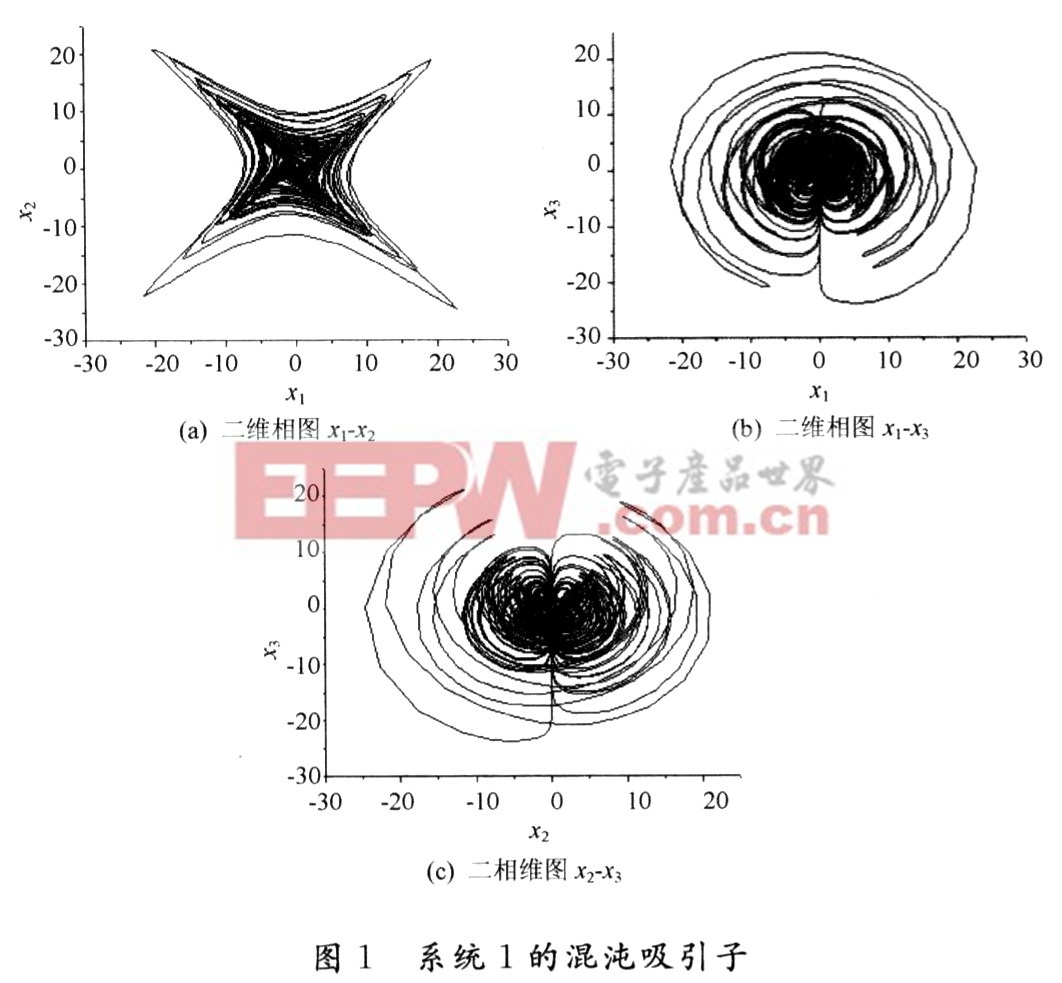
式(1)中,u和a是正的控制參數,當u=2和a=1時系統出現混沌行為。圖1所示為系統1的典型混沌吸引子。由圖可見,系統1的混沌吸引子除具有低維混沌吸引子的一般特點外,還具有其獨特之處;吸引子的二維投影具有更復雜的折疊和拉伸軌線。這說明系統1在局部上比低維混沌系統具有更強的不穩定性。這使得對系統1的控制難度大大增加。
2 控制器的設計
對系統1施加控制,使系統的狀態變量xi(i=1,2,3)追蹤給定參考信號,受控后的系統方程為:
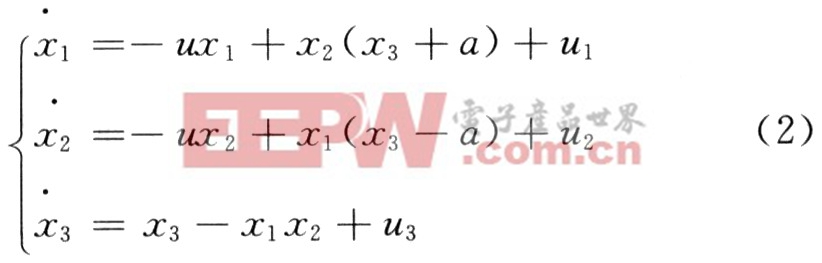
不論參考信號的形式如何,設計如下統一形式的控制器:

式中,r1,r2,r3為給定參考信號。
定理 對于受控系統2,當采用式(3)所示的控制器時,系統狀態變量xi(i=1,2,3)可以追蹤任意連續可微的參考信號ri(i=1,2,3)。
證明 設追蹤誤差變量為ei=xi一ri(i=1,2,3),結合式(2)和式(3),可得追蹤誤差系統為:

式(4)的平衡點為(0,O,O)。由式(4)可知,誤差變量的零點即為誤差系統的平衡點。式(4)在平衡點處的Ja―cobian陣為:

特征方程為:(λ+u)(λ+u)(λ+1)=O,可解得矩陣J的特征根為λ1=一u,λ2=一u,λ2=一l,由于參數“為正,所以矩陣J的所有特征根均為負數。由非線性系統的線性化穩定理論,誤差系統的零解漸近穩定。即lim|ei|=0。
3 數值仿真
3.1 追蹤常值信號
系統1有5個平衡點,分別為S0(0,0,0),S1(1.175 6,一1.902 1,一2.236 1),S2(一1.175 6,1.902 1,一2.236 1),S3,4(±1.902 1,±1.175 6,2.236 1)。取參考信號為系統平衡點S1,即r1=1.175 6,r2=一1.902 1,r3=一2.236 1。由式(3)得控制器為:
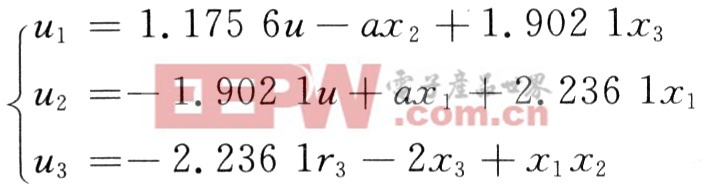











評論