本論文結合上述情況，在某項目中總結出了一套對PID算法的參數進行整定的方法。PID調節方法是三階系統中一種常用的有效控制方法。PID在許多系統中能夠得到廣泛的運用是由于這些系統都存在非線性和未知的干擾，尤其是在模擬和數字的混合系統中，由于模擬信號很容易受到影響，導致系統設計較為復雜。在一些相互合作的項目中，由于存在單位之間需要保密的原因，對系統的理論分析通常不能夠做到具有精確的數學模型，因此，PID算法是解決這類情況的一種有效控制方法。

1 傳統數字PID算法

1.1 位置式控制算法

位置式PID控制算法描述為：

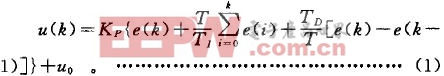
令則離散化的PID位置式控制算法的編程表達式為：

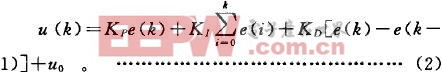
式中：k――采樣序號；
u(k)――第k次采樣時刻的計算結果；
e(k)――第是次采樣相對目標位置的偏差值；
Kl――積分系數；
KD――微分系數；
KP―― 比例系數；
TI――積分時間常數；
TD――微分時間常數；
T――采樣周期。

由式(2)可以看出，每次輸出與過去的狀態有關，要想計算u(k)，不僅涉及到e(k－1)，且須將歷次相加。故用式(2)計算復雜，浪費內存。控制從手動切換到自動時，必須先將計算機的輸出值設置為原始閥門開度uD，才能保證無沖擊切換。

1.2 增量式控制算法

增量式PID控制算法描述為：

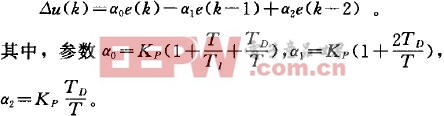
增量式只需計算增量，當存在計算誤差或精度不足時，對控制量計算的影響較小。由于算式中不出現uO，易于實現手動到自動的無沖擊切換。此外，在計算機發生故障時，由于執行裝置本身有寄存作用，故可仍然保持在原位。

基于以上兩種常規的算法，我們在實際應用中又提出了多種改良的算法。在本項目中采用了積分分離PID控制算法。

2 積分分離PID算法

積分分離控制算法的數學模型如下：

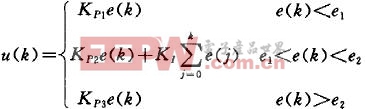
其中，e1、e2分別表示左、右的區間，即離目標位置的距離，這是常規積分分離PID控制算法。在實際的應用中可以根據不同的系統和實際情況再度進行分段。3 位置伺服系統中的算法