電力系統混沌振蕩的自適應最優控制

 本文引用地址:http://www.j9360.com/article/162414.htm
本文引用地址:http://www.j9360.com/article/162414.htm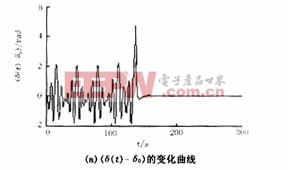
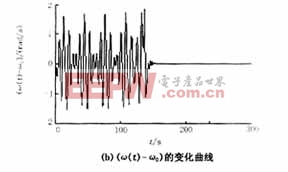
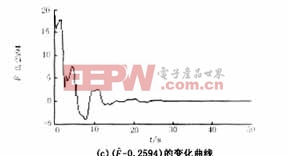
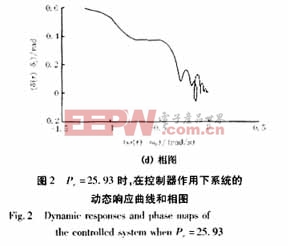
現針對這兩種情況,考慮式(7)所示的控制器的作用。當Pe=25.93(F=Pe/H=0.2593),系統處于混沌狀態運行100s后,投入控制器,受控系統的動態響應以及相圖(δ(t)-δ0)與(w(t)-w0)關系曲線)如圖2所示。由圖2可見,在控制器的作用下,系統的混沌振蕩得到了迅速的抑制,而且系統回到了初始平衡點,受控系統能夠迅速的辨識周期性擾動的幅值,為清楚顯示受控系統對參數的辨識能力,圖2(c)中只給出了加入控制器后50s以內,F-0.2593的變化情況。
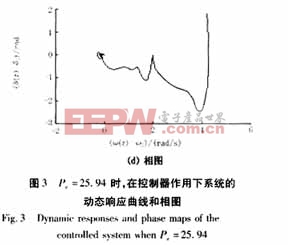
當Pe=25.94(F=Pe/H=0.2594),系統失去穩定之前(t=137s時)投入控制器,受控系統的動態響應以及相圖如圖3所示。由圖3可見,在控制器的作用下,系統迅速地進入穩定狀態,而且回到了初始平衡點,受控系統也能夠迅速的辨識周期性擾動的幅值。
4 結論
由于自適應最優控制方法能夠辨識系統所受周期性擾動的幅值,因此在該控制器的作用下,無論周期性負荷擾動的幅值是否已知,系統均能夠回到初始平衡點,維持電力系統的穩定性,同時在自適應最優控制器的設計中假定系統是未精確建模的,因此該控制方法對系統模型的精確性沒有提出很高要求,比其它的非線性反饋方法具有優越性,也可以應用在電力系統其它控制器的設計中。



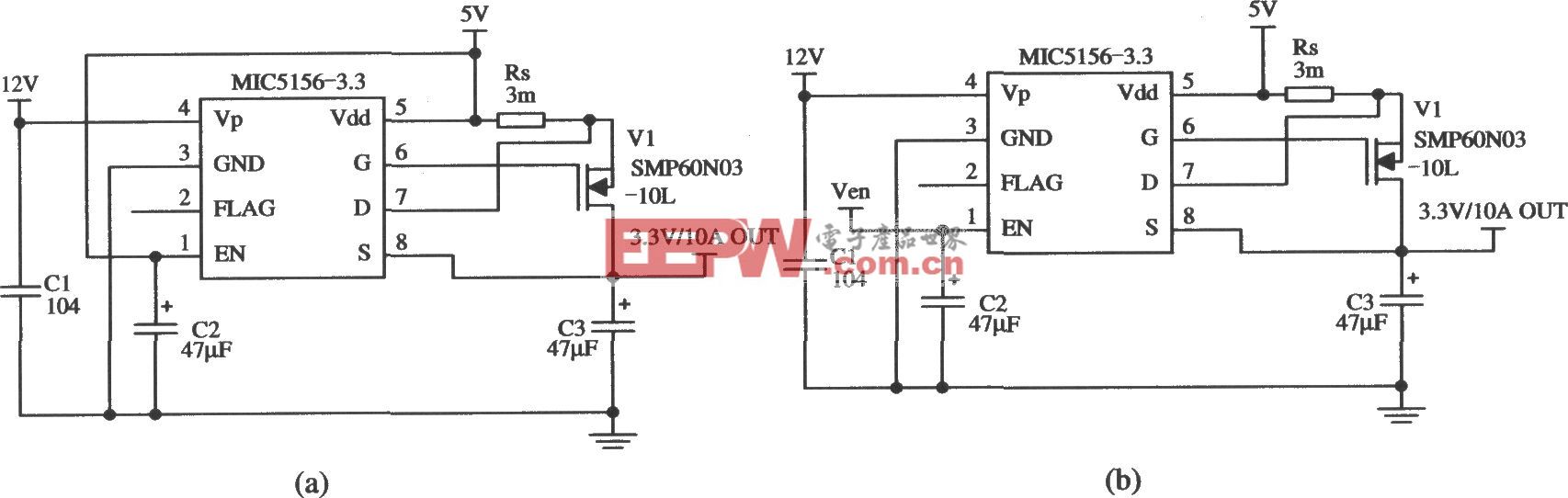
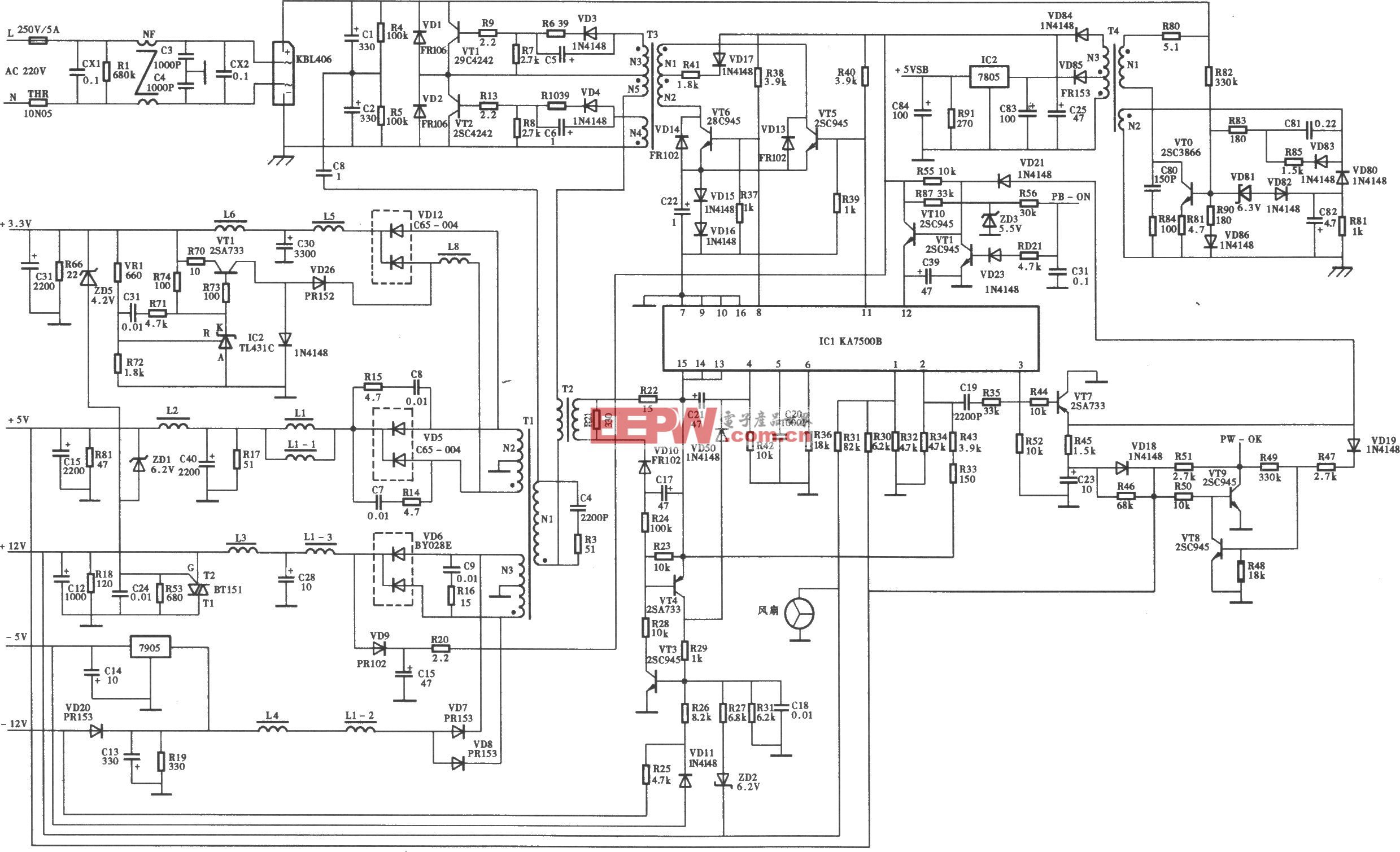
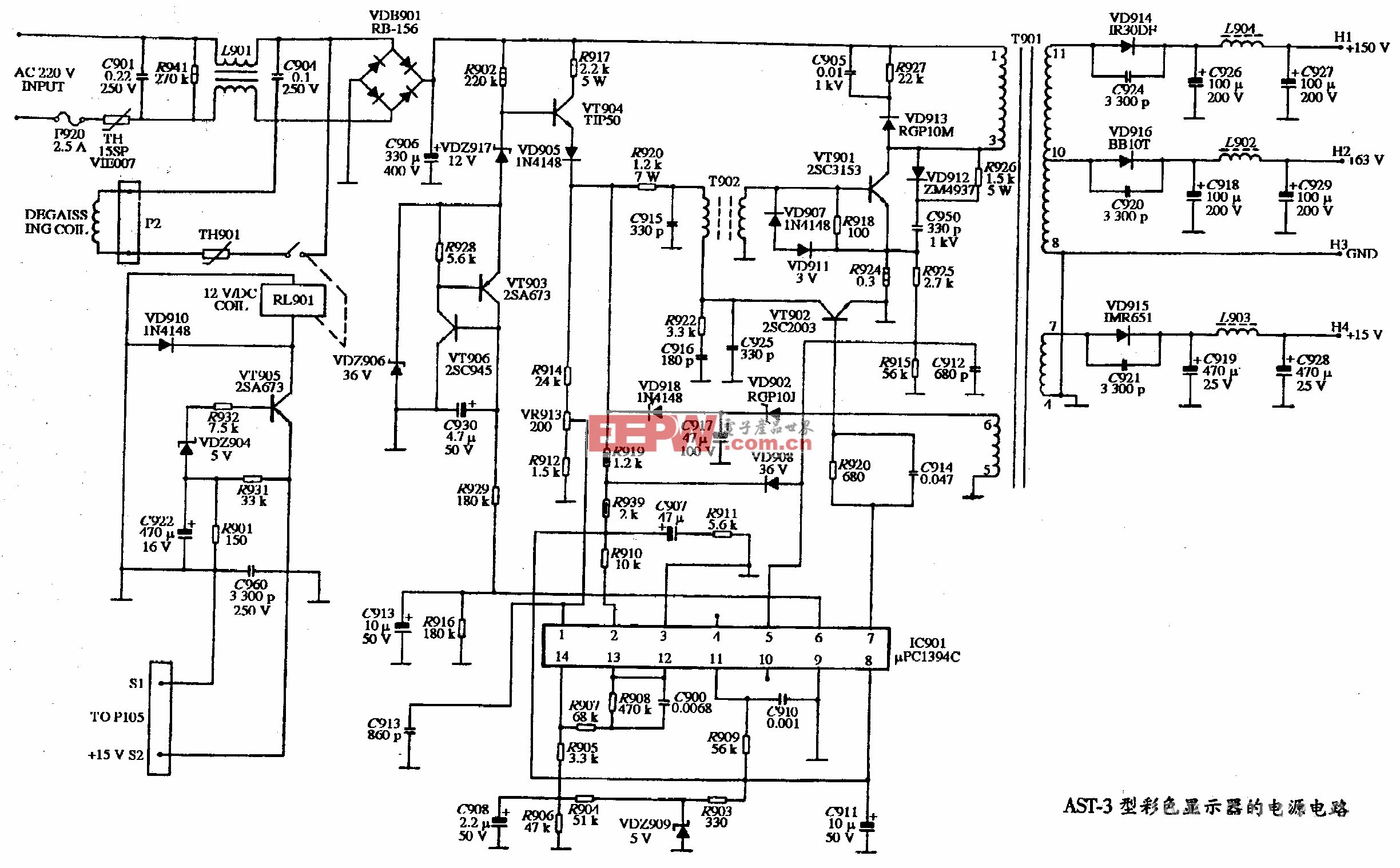


評論