摘要：通過深入研究云模型相關文獻，提出一種在西門子S7-300 PLC上實現一維正態云模型的方法，在編程軟件STEP7中用STL語言編寫標準正態隨機數、一維正態云模型算法等功能及其他相關程序，最后通過STEP7、PLCSIM和WINCC進行聯合仿真測試，測試結果表明在S7-300 PLC上能實現一維正態云模型算法。
關鍵詞：一維正態云模型；視窗控制中心；可編程控制器；隨機數

自1995李德毅院士正式提出隸屬云慨念(即云模型概念)以來，云模型理論的基本框架及其算法逐步得到完善，并開始趨向成熟。目前云模型的硬件實現已成為研究熱點，如云模型已被用于TMS320F2812 DSP和STC89C52單片機[2—3]。PLC自1968年問世以來，憑借其可編程性、高可靠性成為工業自動化領域應用最廣泛的控制設備。在深入研究云模型相關資料時，發現實現云模型的前提條件是能進行四則運算及指數、對數運算和產生任意正態隨機數。S7-300 PLC運算功能強大，具有進行四則運算及指數、對數運算功能。但S7-300 PLC并沒有產生隨機數的硬件模塊、系統功能SFC和系統功能塊SFB。在深入分析隨機數生成相關文獻的基礎上，用STL語言在SIEMENS編程軟件STEP7上編制一個個功能FC實現任意正態隨機數的產生，一維正態云模型算法等，最后在SIEMENS PLC專用的仿真器PLCSIM上進行調試，并將輸出過程值用組態軟件WINCC進行歸檔，然后將歸檔數據導入EXCEL，再將EXCEL里的數據轉換成圖形進行直觀驗證。

1 云模型
1．1 云模型的定義
設U={x}是一個用精確數值表示的定量論域，T是U上的定性概念即語言子集，CT(x)是U到閉區間[0，1]的映射，對于任意x∈U，都存在一個有穩定傾向的隨機數CT(x)，則稱式(1)為云模型。

特別地，設R1(E1，E2)表示服從正態分布的隨機數，其中E1為期望值，E2為標準差，則由滿足式：

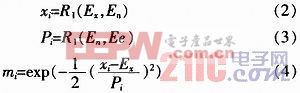
數據對drop(xi，mi)(i=1，2，…N)構成的云模型稱為一維正態云模型，簡稱一維正態云，組成云模型的數據對(xi，mi)稱為一維云滴。其中，Ex、En和He為云模型的3個重要數字特征，分別成為期望值、熵和超熵，記為[Ex，En，He]。
1．2 一維正態云模型算法
一維正態云模型其輸入為表示定性概念的期望值Ex、熵En和超熵He，云滴數量N，輸出是N個云滴在數域空間的定量位置及每個云滴代表該概念的確定度。具體算法為輸入：(Ex，En，He，N)
輸出：drop(x1，m1)，drop(x2，m2)，…，drop(xN，mN)
1)生成以Ex為期望值，En為標準差的一個正態隨機數xi=R1(Ex，En)
2)生成以En為期望值，He為標準差的一個正態隨機數Pi=R1(En，He)
3)計算：
4)令數據對(xi，mi)為一個一維云滴。
5)重復步驟1)～4)，直至產生N個云滴。

2 正態分布隨機數產生器
正態分布又稱高斯分布，是最重要、最常見、應用最廣泛的一種連續型分布一般來說，具有任意分布的隨機數都是由(0，1)區間上的均勻分布隨機數來實現的因此，首先要生成(0，1)區間上的均勻分布隨機數，然后再利用隨機變量函數變換的方法產生正態分布的隨機數。
2．1 (0，1)均勻分布隨機數生成方法
(0，1)區間上的均勻分布偽隨機數產生的方法多種多樣，有線性同余法、平方取中法、混沌法、反饋移位寄存器法等，其中最常用的是線性同余發生器，它通過如下的線性同余遞推關系式來產生數列。

其中，a，c，x0，M均為正整數，x0為種子，使用時需要仔細地挑選模數M和種子x0，使得產生出的偽隨機數的循環周期要盡可能長。xi為(0，1)區間上的隨機數。
2．2 正態分布隨機數的生成方法
生成(0，1)均勻分布隨機數后，可以通過反函數法、變換法、舍選法、組合法等各種變換及映射關系來得到任意正態分布隨機數。下面具體介紹變換法。
變換法通過一個變換將一個分布的隨機數變換成為不同分布產生的隨機數，變換法的典型的例子是Box-Muller變換，它可產生精確的正態分布隨機變量。其變換式為：

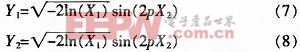
X1、X2是在區間[0，1]上均勻分布的隨機變量，所得的Y1、Y2相互獨立的均勻值，方差的正態分布隨機變量。