摘要：為了正確反映基于光電位置敏感器(PSD)的微位移傳感器的特性，首先介紹了一維光電位置敏感器的工作原理并分析了利用PSD結合光學三角測量法將位移信號轉換成電壓信號的工作原理，得出基于PSD的微位移傳感器被測試件位移量與相關測量電路輸出電壓(S，V)關系特征，然后基于最小二乘估計算法基本原理，提出了運用MATLAB語言建立PSD的微位移傳感器(S，V)關系特征的數學模型的方法，給出了建模的程序流程圖以及仿真結果。
關鍵詞：光電位置敏感器；微位移傳感器；傳感器建模；位移測量；MATLAB語言

位置敏感傳感器(position sensitive detector，PSD)廣泛應用于光學位置、角度的測量與控制、工業自動化生產、遠程光學控制系統、微電子生產中的各類檢測和監控、位移和振動監測等。在PSD的眾多應用領域中，應用最為廣泛的就是位移測量。本文通過光學三角測量的方法將測量物理位移信號轉換成PSD能夠測量的位移信號，然后利用PSD工作原理將位移信號轉換成電流信號，通過后續電路將電流信號轉換成電壓信號，經過放大、濾波、A／D處理后交由計算機對采集得到的電壓(V)和位移(S)信號進行處理。為準確反映該PSD的微位移傳感器系統的V-S間關系，實現精確測量，需要擬合出一條曲線盡可能逼近PSD的微位移傳感器實際的輸入、輸出特性。文中采用MATLAB語言，運用矩陣運算，由實驗測得數據采用分段擬合的方法建立了PSD的微位移傳感器V-S間的數學模型，對于PSD的微位移傳感器實際的非線性特性進行擬合，逼近得出最佳關系曲線。

1 基于PSD的微位移傳感器測量原理分析
1．1 PSD的工作原理
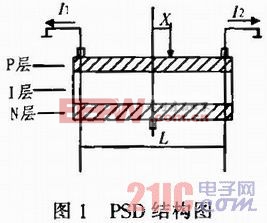
PSD分為一維PSD和二維PSD。一維PSD大致分為P-I-N 3層。一維PSD截面如圖1所示。表面P層為感光面，從P層兩側分別引出一個電極，作為輸出。中間的I層為電離層。底面N層的引出一個電極，作為公共端并施加反偏電壓。PSD的光敏層接受入射光照射時，在相應的入射位置上所產生的電荷與光能成正比例關系，電荷定向移動形成光電流由P層兩個輸出電極輸出。2個電極輸出的電流大小都與入射光點位置到各電極之間距離有關，若感光面電阻是均勻分布的，距離越大，光電流越小；反之，則越大。

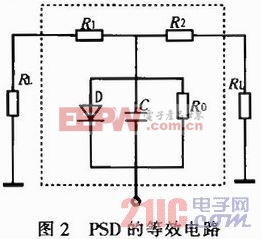
PSD的等效電路如圖2所示，設電極1和電極2的距離為L，電極1和電極2輸出的光電流分別為I1和I2，則電極3上的電流為總電流I0，并且IL=I1+I2。若以PSD的中心點位置作為原點，光點離中心點的距離為X。對一維PSD，如果負載電阻與面電阻相比很小，則有式(1)關系：

由式(1)可以看出光點坐標X僅和兩極輸出電流有關，而和入射光點強度無關，因此，若可以通過實驗測量獲得參數I1和I2的數值，光點坐標X就是可求的。

1．2 光學三角法構成的位移尺寸傳感器
PSD進行位移測試時經常采用光學三角測量法。具體過程為：當激光束入射到被測試件表面時，會形成漫反射光斑，將其作為信號，利用透鏡成像原理將收集到的漫反射光會聚到焦平面的光接收器上形成像點。當入射光斑隨被測物面移動時，像點在光接收器上面做相應移動，根據像移大小和系統結構參數可以確定被測物面的位移量。基于PSD的微位移傳感器測試原理由圖3所示。

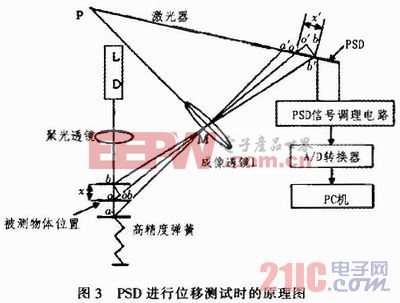
由于直接從電極輸出的是微安級的光電流變化，并且負載電阻應該盡可能小，因此需要合適的信號調理電路對PSD的輸出信號進行處理和運算才能得到位置坐標。本系統的PSD信號調理電路主要由前置放大器、加法器、減法器、除法器等構成。其中包含4個高精度運算放大器。兩個作為前置放大運算放大器，將電流信號轉換成電壓信號進行放大，放大倍數取決于反饋電阻阻值。本系統在調試時為了提高測量精確度采用了精確阻值的電阻。另外兩個高精度運算放大器分別作為加法器和減法器，為了實現精確測量，盡可能避免軟件方法實現的除法器在兩路數據采集過程中難以真正實時同步的缺點，本系統采用高精度模擬除法器實現除法運算功能。由于加法器、減法器、除法器的輸出具有一定的電壓波動，所以系統還加入了濾波器。用數據采集卡PCL-818HD采集高精度模擬除法器的輸出電壓并實現A／D轉換，通過編程實現轉換結果和PC機中的MATLAB數據連接，通過調用自行編寫的建模程序實現對基于PSD的微位移傳感器的建模，即在傳感器系統中，電壓大小與光點位置和原點之間的距離近似成線性比例關系。

2 用MATLAB語言建立數學模型原理
實驗過程中所得到的實驗數據往往是離散的，傳感器建模的最終目標是通過某些擬合方法得到輸入量與輸出量之間的連續光滑曲線。實際測得一組傳感器測量數據集{Xk，Yk}，(k=1，2，…n)，其中Xk為被測量，Yk為傳感器輸出量。基于最小二乘法的傳感器數學模型的建立，就是要用多項式(2)

擬合測量數據集{Xk，Yk}，(k=1，2，…n)，使φ值最小。一般均采用歐氏范數‖δ‖2作為誤差度量的標準。使用MATLAB的M語言對最小二乘算法進行編程，通常采用兩種方法：利用polyfit函數進行多項式擬合，或利用矩陣除法解決復雜函數的擬合。文中用第一種方法擬合基于PSD的微位移傳感器的數學模型。函數polyfit的輸入量為X、Y、n，其中X、Y即為需要建立相互關系的2個變量的測量值，以數組的形式輸入，n為多項式的階數，輸出的是多項式系數的行向量，得到的多項式是降冪的。對給定的一組數據(Si，Vi)(i=0，1，…，n)，選取線性無關的基函數φ={S0，S1，…，Sm}，要求由φ中找出一個函數y=V*(S)，使誤差平方和



3 基于MATLAB語言的傳感器建模流程
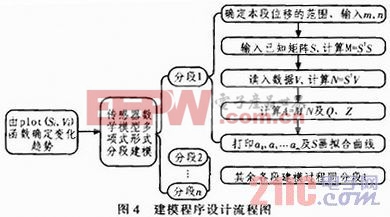
通過對某PSD的微位移傳感器建模原理的分析，利用MATLAB語言對傳感器進行建模步驟為：
1)實際測得一組實驗數據(Si，Vi)(i=0，1，…，n)(以數組形式輸入這樣便于在計算過程中引用)，利用MATLAB中的plot(Si，Vi)函數完成描點畫圖，大致確定傳感器系統輸出電壓和被測試件位移量之間變化趨勢。
2)根據傳感器系統輸出電壓和被測試件位移量之間變化趨勢，采用分段建模方式確定PSD的微位移傳感器數學模型為多項式形式如式(8)所示：
V(S)≈a0+a1S+…+amSm (8)
3)選取基函數為φ={1，S，S2，…，Sm}，建立位移矩陣S。
4)將電壓矩陣和位移矩陣代入相應法方程。
5)求解矩陣A。
①輸入實驗測得電壓數據、實驗次數n’=n+1及擬合多項式階數m②求ST及M=STS③求N=STV④求A=M-1N6)求Q值及Z值。
建模程序設計流程圖如圖4所示。

4 實例分析與仿真
完成系統硬件連接，并對系統進行調試，開始對數據進行采集。實驗過程中，利用步進電機對系統位移進行改變，步進電機精度為0．1 μm，其值遠小于步進電機的步距(步距為10μm)故可以認為位移值為真值。為了提高檢測的精確度，減小隨機誤差，PC機所獲取的測量值為對每個檢測點進行連續20次測量所取的平均值，其精度足以滿足要求。通過實驗測得PSD的微位移傳感器系統輸出電壓和被測位移量之間對應關系的一組數據如表1所示。(電壓采用20次測量的均值)。

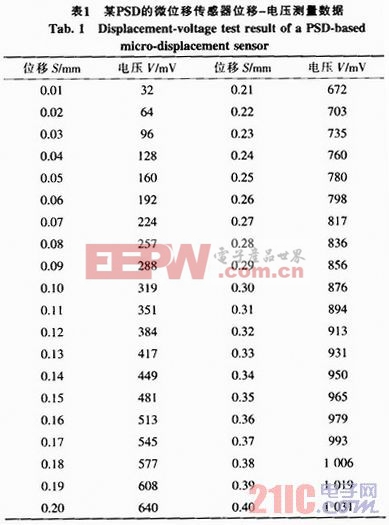
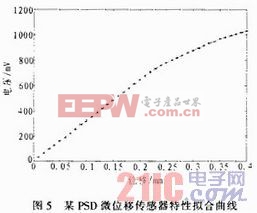
由實驗數據可知：在PSD的中間區域內，V-S變化趨勢基本上成線性關系；但是在被測試件位移量較大和接近PSD的邊緣時，兩個區間內線性度較差，呈現非線性關系，這主要因為影響傳感器特性的因素有很多；PSD器件的固有特性決定其存在非線性，這也是其主要不足之處另外，PSD不是理想的點電極，電極之間并非對稱，而且，入射光、反偏電壓、背景光、環境溫度等都是影響傳感器特性的因素。故大致可以分3段擬合該PSD微位移傳感器的數學模型。擬合后殘差平方和的大小決定了多項式擬合的效果，為了盡可能降低各測量點的殘差平方和的數值，要合理選擇擬合的階次。擬合階次的選擇既要兼顧擬合曲線的光滑程度，又要注重考慮真實反映傳感器輸入、輸出之間的變化規律。某PSD的微位移傳感器特性擬合曲線如圖5所示。

5 結論
PSD的微位移傳感器的輸出電壓和被測試件位移間存在對應關系。通過合理選擇測量點，相應測得一組實驗數據，運用MATLAB語言對PSD微位移傳感器建立其數學模型，擬合求出PSD微位移傳感器的(S，V)曲線。仿真結果表明，利用這種建模方法可以實現PSD微位移傳感器數學模型階次和系數的辨識，擬合出的(S，V)曲線較為直觀地反映了某PSD微位移傳感器的特性，具有較高的擬合精度。此種建模方法具有良好的通用性，富于實際意義。PSD微位移傳感器的模型的建立為其非線性補償問題找到了一個很好的途徑。