摘要：多參量多點實時監測顯示是傳感研究領域的一項重要技術。以光纖Fabry-Perot(F-P)腔與光纖Bragg光柵(FBG)傳感器的串聯復用結構為單元構建空分復用(SDM)系統，設計了溫度、應力多點實時顯示的方案。由FPGA構建的SOPC與NiosⅡ完成對多監測點的數據采集，由VB串口通信接收FPGA存儲器存儲的采集數據，再把此數據由高斯曲線擬合方程處理得到溫度和應力的參數值，最后用VB實現監測顯示。結果表明F-P腔與FBG串聯能有效克服溫度與應力的交叉敏感，FPGA結合VB能很方便的實現多參量多點的實時監測顯示。
關鍵詞：光纖傳感；空分復用；溫度與應力顯示；FPGA；VB

0 引言
近年來，光纖光柵傳感技術的應用在各行各業中得到了快速的發展。人們對待測物理量在精度、性能、容量以及多參數等方面提出了更高的要求。這極大地促進了光纖光柵傳感復用類型相關理論和技術的研究，而解調顯示技術正是其中的一個重要環節，現常以ARM，DSP，FP GA等芯片為核心控制多路數據信號的采集、存儲和處理，并用LabVIEW，VB，Matlab及其混合使用等做界面顯示處理。
文中FPGA與VB結合實現多參量的監測顯示，得益于FPGA高度集成、內部資源豐富、功能強大、時序控制精確、支持并行處理、編程靈活等優點；VB簡潔易懂、界面設計簡單。
本文主要完成了對多監測點雙參數監控顯示的研究。FBG能通過反射或透射波長實現對溫度的測量；F-P可用做可調諧F-P腔、濾波器、傳感器等，調節腔長與電壓的關系能實現對應力解調。故首先設計了一種基于FBG與F-P腔傳感器串聯復用，并對其進行空分復用，構建成能實現多監測點雙參數高精度解調的系統。分析F-P腔與FBG串聯復用的光譜，可知能實現待測信號的高精度解調：即F-P腔長(應力)和FBG反射中心波長(溫度)的同時測量。并使用FBG和F-P腔分別對溫度與應力進行測量，進而與F-P腔和FBG串聯復用所得結果進行比較，通過實驗對該方法進行了驗證。而空分復用就能實現多個監測點的雙參數高精度解調。此后由FPGA構建的SOPC與NiosⅡ完成對多監測點雙參數的數據采集；由VB串口通信進行數據接收，并把采集到的數據帶入高斯曲線擬合方程中，求出具體的溫度與應力，并用VB界面實現了監控顯示。

1 原理分析與理論模型
1．1 FBG的應變和溫度響應
根據光纖耦合模型理論可知，滿足Bragg條件的反射光波長為：
λB=2neffΛ (1)
式中：Λ為光柵周期；neff為有效折射率。當Λ和neff因外界同時引起較小的變化ΔΛ和Δneff時，由Bragg條件可知，反射波長會發生移位ΔλB。ΔλB可表示為：
△λB=2△neffΛ+2neffΔΛ (2)
若溫度、應變共同作用時，產生的Bragg波長位移ΔλB，用線性關系可表示為：

式中：α是光纖材料的熱膨脹系數；△T是溫度變化量；pmn為材料的光彈系數；v2，v3為泊松比。由式(3)可知，由單一FBG在測得中心波長移動ΔλB時，還需知道溫度才能求出應變，這就是溫度與應變的交叉敏感問題。當應變和溫度同時發生變化時，光纖光柵無法區分由二者獨自引起的波長變化，測量其中一個量時，總會受到另一個量的影響。為解決交叉敏感問題，人們提出了多種方法，其中串聯復用傳感就是一種有效的方法。如光纖布拉格光柵和長周期光柵結合的傳感器系統，該系統能實現油氣井下應力和溫度的同時測量。本文研究F-P腔與FBG串聯復用傳感，能消除交叉敏感影響，并對該串聯復用傳感器進行空分復用實行多點監測，最終用VB編碼實現數值界面顯示。
1．2 F-P腔與FBG串聯復用傳感器的解復用
因為F-P腔有溫度-壓力交叉敏感性能實現對溫度的補償，能使測量精度提高，故可采用F-P腔與FBG串聯復用傳感器的解復用。其結構如圖1所示。

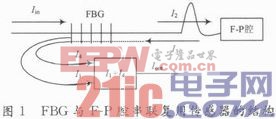
原理闡述：光從光纖左端入射Iin，進入FBG與F-P腔串聯復用的結構中，首先經過FBG溫度傳感器，此時Bragg反射波長附近的一部分光I1被反射，而透射光I2入射到F-P腔傳感器，得到F-P反射光譜為一低反襯度的F-P腔干涉光譜I3，I3再通過FBG傳感器，其透射光部分為I4。與之前的FBG傳感器反射光I1相疊加形成最終的輸出光譜Iout。其數學表達式為：
Iout=I1+I4=Iin[fFBG+(1-fFBG)2fF-P] (4)
式中：fFBG=R·exp[-(λ-λB)2／c2]，即用高斯分布來表示FBG的反射譜，R為光柵峰值反射率；λB為Bragg反射中心波長；c值的大小用于表征反射峰的寬度；fF-P=2r[1+cos(4πL／λ+π)]，其中r為光纖端面反射率。L為F-P腔的腔長，λ為光波長。
由式(4)可知，由傳感器返回的光譜并不是FBG傳感器與F-P腔傳感器各自反射光譜的簡單疊加。此時，若直接采集光譜信號中的FBG反射峰值波長作為FBG傳感器的溫度解調信號，將導致結果發生偏差，影響溫度測量精度。為了得到精確的FBG反射光譜信號，將式(4)展開成為關于fFBG的一元二次方程：

解此方程，可得精確的FBG反射光譜，進而通過對解出的光譜峰值部分進行高斯擬合，求解出中心位置，即可解出FBG的中心波長。式(5)中Iout和Iin是可直接測量得到的光譜分布數據，fF-P通過F-P腔反射光譜的交叉相關解調算法得到。消除FBG對F-P腔解調的影響只需找到FBG的粗略峰值位置，將FBG峰值部分光譜數據從光譜中扣除。由于FBG光譜寬度遠小于寬譜光源寬度，而交叉相關計算對于小范圍光譜數據的缺失不敏感，因而不影響F-P腔解調結果的精度。