3 程序設計和精度問題
3．1 程序設計
此設計中的DSP主要用于微分數值的迭代運算，其計算性能將決定信號產生速度，這里采用TI公司的TMS320C5402型低功率器件作為核心，其速度可達100 MI/s，以Lorenz方程為例，其方程如下：

式中，參數值分別為：α=5．5，β=-7．4，k1=0．25，k2=0．1。
圖2為系統程序流程。

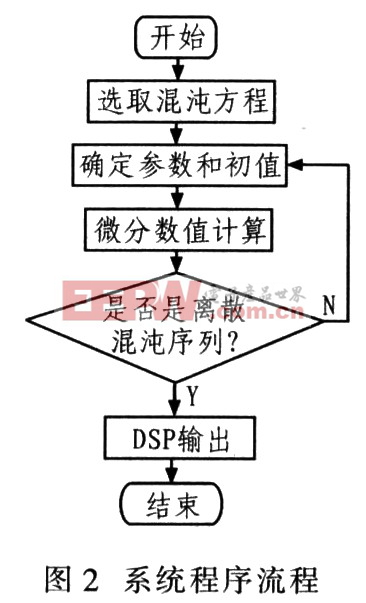
3．2 精度問題
混沌信號的產生主要借助于：DSP強大的運算能力，采用數值計算方法，可根據不同的精度要求選用不同的方法。精度越高，運算量越大，則混沌信號的頻率越低，所以要根據實際需要選取合適的精度。混沌方程的微分數值計算方法主要有：歐拉方法、改進歐拉方法及四階龍格一庫塔法。這3種方法精度由低到高，計算量也由低到高。運算量的大小直接決定運算速度，即決定混沌信號的產生速度。選用何種計算方法取決于對精度和速率的要求以及對運算量的承受能力。上述核心程序采用四階龍格一庫塔法。

4 信號的驗證與測試
4．1 信號驗證
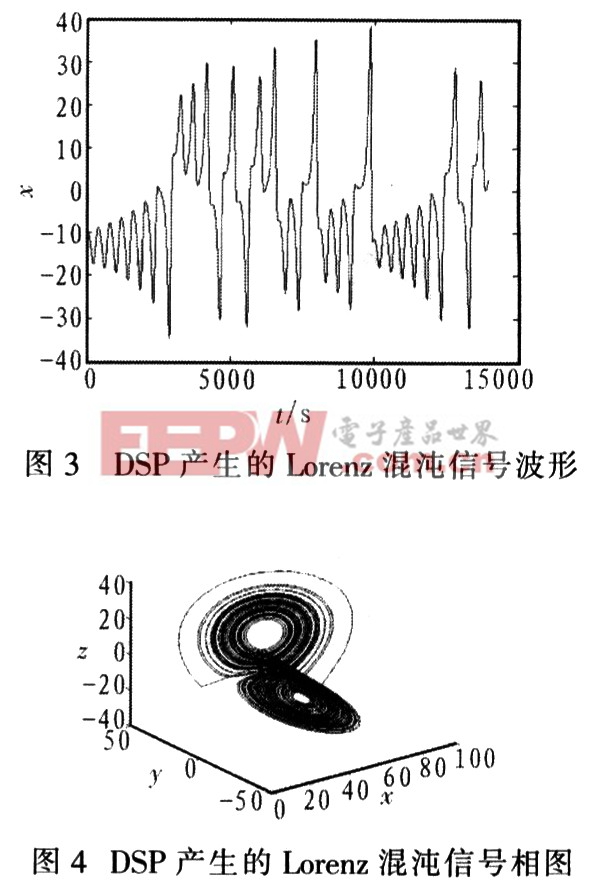
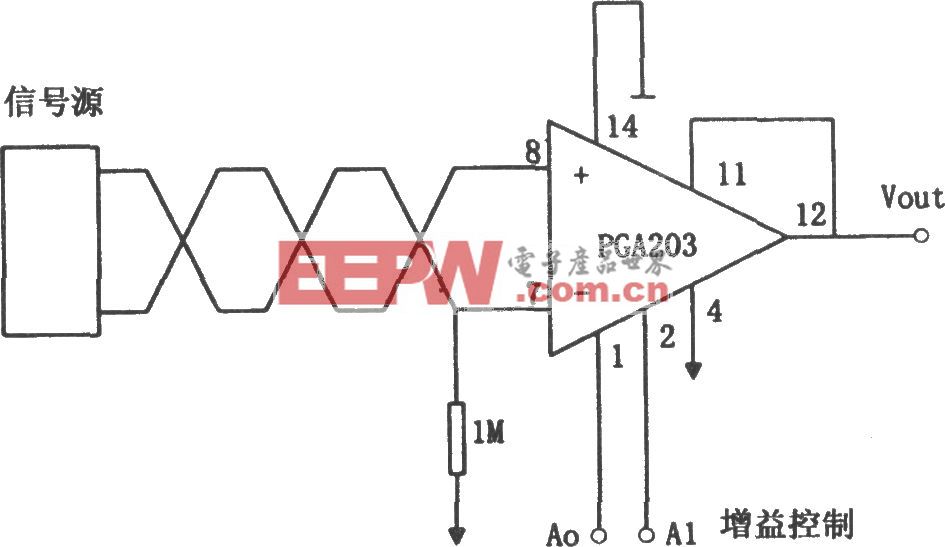
產生的信號是否為混沌信號必須經過驗證。判斷混沌信號的方法很多，但都存在需要復雜運算的問題。一般情況下通過示波器顯示的單通道波形很難判斷混沌與否。MATLAB和TI公司聯合開發的MATLAB Link for CCS Development Tool(簡稱CCSlink)工具箱更適合于程序的調試，對混沌信號的驗證不夠靈活。這里采用一種簡單有效的方法判斷DSP產生的信號是否混沌。運用 JTAG測試技術和CCS的在線調試功能，直接訪問DSP內存。以Lorenz混沌信號的檢測為例，在CCS編譯環境的程序部分通過設定，將數據X存在 DSP的地址0X0088，Y存在地址0X0099，Z存在地址0X00A0，使用探針功能采集內存中的數據，并將其存為DAT文件格式，然后利用 Matlab強大的圖形能力對數據進行處理，通過分析相圖判斷信號是否為混沌信號。這里共采集98 047個點的數據。利用Matlab方法將采集到的DSP產生的數據制成波形圖和相圖，分別如圖3、圖4所示。由圖3和圖4易知產生的數據是混沌的，從而驗證了設計的正確性。