蝶形、同址和變址計算方法及公式
1. 蝶形計算
任何一個N為2的整數冪(即N=2M)的DFT,都可以通過M次分解,最后成為2點的 DFT來計算。M次分解構成了從x(n)到X(k)的M級迭代計算,每級由N/2個蝶形組成。圖3.20表示了蝶形的一般形式表示。
其輸入和輸出之間滿足下列關系:

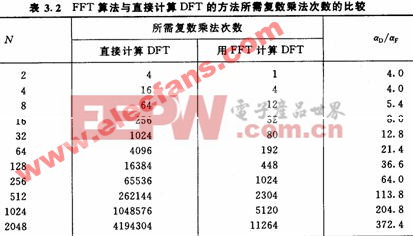
大多數情況下復數乘法所花的時間最多,因此下面僅以復數乘法的計算次數為例來與直接計算進行比較。
直接計算DFT需要的乘法次數為αD=N2,于是有 例如,當N=1024時,則:
例如,當N=1024時,則: 205,即直接計算DFT所需復數乘法次數約為FFT的205倍。顯然,N越大,FFT的速度優勢越大。
205,即直接計算DFT所需復數乘法次數約為FFT的205倍。顯然,N越大,FFT的速度優勢越大。
同址(原位)計算
圖3. 19包含log2N級迭代運算,每級由N/2個蝶形計算構成。蝶形計算的優點是可以進行所謂同址或原位計算。
現在來考察第一級的計算規律。設將輸入x(0),x(4),x(2),x(6), x(1),x(5),x(3),x(7)分別存入計算機的存儲單元M(1), M(2), M(3),…,M(7)和M(8)中。首先,存儲單元M(1)和M(2)中的數據x(0)和x(4)進入運算器并進行蝶形運算,流圖中各蝶形的輸入量或輸出量是互不相重的,任何一個蝶形的二個輸入量經蝶形運算后,便失去了利用價值,不再需要保存。這樣,蝶形運算后的結果便可以送到M(1)和M(2)存儲起來。類似地,M(3)和M(4)中的x(2)和x(6)進入運算器進行蝶形運算后的結果也被送回 到M(3)和M(4)保存,等等。第二級運算與第一級類似,不過,M(1)和M(3)存儲單元中的數 據進行蝶形運算后的結果被送回M(1)和M(3)保存,M(2)和M(4)中的數據進行蝶形運算 后送回M(2)和M(4)保存,等等。這樣一直到最后一級的最后一個蝶形運算完成。
蝶形運算的特點是,首先每一個蝶形運算都需要兩個輸入數據,計算結果也是兩個數據,與其它結點的數據無關,其它蝶形運算也與這兩結點的數據無關、因此,一個蝶形 運算一旦計算完畢,原輸入數據便失效了。這就意味著輸出數據可以立即使用原輸 人數據結點所占用的內存。原來的數據也就消失了。輸出、輸人數據利用同一內存單 元的這種蝶形計算稱為同位(址)計算。
可以看出, 每一級的蝶形的輸入與輸出在運算前后可以存儲在同一地址(原來位置上)的存儲單元中,這種同址運算的優點是可以節省存儲單元,從而降低對計算機存儲量的要求或降低硬件實現的成本。
3.變址計算
從圖3. 19所示的流程圖看出,同址計算要求輸入x(n)是“混序”排列的。所謂輸入為“混 序”,并不是說輸入是雜亂無章的,實際上它是有規律的。如果輸入x(n)的序號用二進制碼來 表示,就可以發現輸入的順序恰好是正序輸入的“碼位倒置”,表3. 3列出了這種規律。
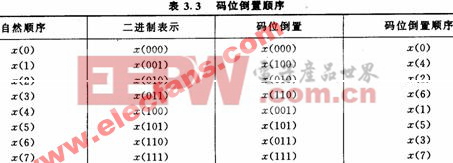
在實際運算中,按碼位倒置順序輸入數據x(n),特別當N較大時,是很不方便的。因此,數據總是按自然順序輸入存儲,然后通過“變址”運算將自然順序轉換成碼位倒置順序存儲。實現這種轉換的程序可用圖3. 21來說明。

圖中用n表示自然順序的標號,用l表示碼位倒置的標號。當l=n時,x(n)和x(l)不必互相調換。當l≠n時, 必須將x(l)和x(n)互相調換,但只能調換一次,為此必須規定每當l>n時,要將x(l)和x(n)相互調換,即把原來存放x(n)的存儲單元中的數據調入存儲x(l)的存儲單元中,而把原來存儲x(l)的存儲單元中的數據調入到存儲x(n)的存儲單元中。
這樣,按自然序輸入的數據x(n)經過變址計算后變成了碼位倒置的排列順序,便可進入第一級的蝶形運算。
最后介紹一下時間抽選FFT算法的另外一些形式的流程圖。對于任何流程圖,只要保持 各節點所連支路及其傳輸系數不變,則不論節點位置怎樣排列,所得到的流程圖總是等效的,因而都能得到DFT的正確結果,只是數據的提取和存儲次序不同而已。
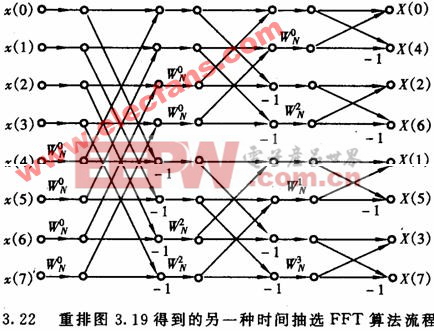
把圖3. 19中與x(4)水平相鄰的所有節點和與x(1)水平相鄰的所有節點交換,把與x(6)水平相鄰的所有節點和與 x(3)水平相鄰的所有節點交換,而與x(2)、x(5)和x(7)水平相鄰各節點位置不變,就可以從圖3. 19得到圖3.22。圖3.22與圖3.19的區別只是節點的排列不同,而支路傳輸比,即WN的 各次冪保持不變。顯然圖3.22所示流程圖的輸入是正序(自然順序)排列的,輸出是碼位倒置 排列的,所以輸出要進行變址計算。圖3. 22所示的流程圖相當于最初由庫利和圖基給出的時 間抽選算法。
另一種形式的流程圖是將節點排列成輸入 和輸出兩者都是正序排列,但這類流程圖不能進行同址計算,因而需要兩列 長度為N的復數存儲器。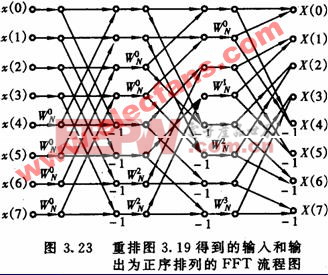















評論