關于多級低通有源濾波器的增益及Q值排序的深入思考
相比之下,設計 2 的階躍響應在級間出現了削波,導致非常不理想的仿真響應結果。這是因為第一級的增益較大導致設計中較早出現了大擺幅。如圖 8 所示,仿真中宏模型正確的預計到第二級的輸出會出現削波,而最后一級將其干凈地濾除了。
本文引用地址:http://www.j9360.com/article/124645.htm
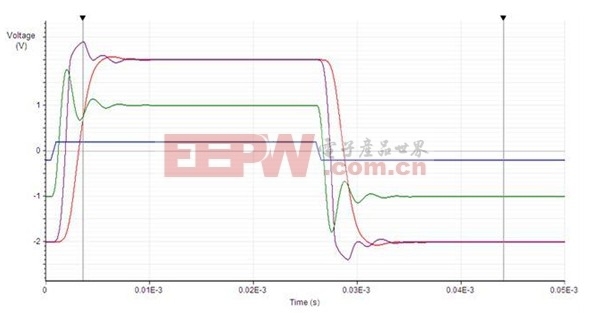
圖 8. 設計 2 的階躍響應出現削波
這明顯比設計 1 的效果差。雖然這是個有些極端的例子,但這也確實說明了用最后一級增益適度來降低級間削波風險的重要意義。
多級濾波器 Q 值排序對噪聲增益峰值的考慮
對曾經測量過 SKF 濾波器輸出噪聲頻譜的人來說,都會有些驚訝地發現噪音峰值有多么高。SKF 濾波器的一項最不為人注意的特性是其高峰值噪聲增益在某種程度上可以通過認真選擇電阻值來減輕。
運算放大器線路的“噪聲增益”指輸出電壓與差分輸入電壓的分壓比的倒數。這說明的是運算放大器自身的輸入噪聲電壓到輸出端的增益的頻率響應。同樣它還是運算放大器開環增益與該噪聲增益的比,即 SKF 濾波器內部通帶頻率上的環路增益。這是極為有用的因子,它說明環路增益越大,諧波失真越低。因此,出于多種原因考慮,應了解并盡力降低 SKF 的噪聲增益峰值。
等式 3 所示的是圖 1 二階低通 SKF 濾波器的噪聲增益拉普拉斯傳遞函數的基本形式。分子是一個二次多項式,實數零分布在較寬的范圍內(一個小于 ω0,一個大于 ω0),但分母的極點是濾波器需要的極點。這個分母的表達式實際上是導入增益元件后的無源2 R和2 C電路的極點等式(將圖 1 中的放大器從電路中去除,讓 C2 接地,就可以得到 C2 之上的從輸入到輸出端的傳遞函數,而這個表達式的極點就是 SKF 噪聲增益表達式的分母)。
等式 3 噪聲增益à
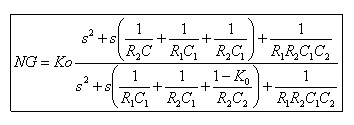
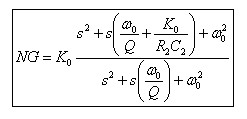
分子等式與所需的濾波器響應一致。如果我們在分母的線性系數中增減 Ko/R2C2 項,然后按濾波器指標項重寫等式,我們會發現實際上我們在噪聲增益響應方面沒有多少裕量。
等式4 濾波器指標項的噪聲增益à
濾波器相關文章:濾波器原理
濾波器相關文章:濾波器原理
低通濾波器相關文章:低通濾波器原理
電源濾波器相關文章:電源濾波器原理
數字濾波器相關文章:數字濾波器原理











評論