基于載流導線循跡智能車的數學模型
張博達 廈門大學嘉庚學院 (福建漳州 363105)
本文引用地址:http://www.j9360.com/article/113805.htm摘要:本文給出了一種方法,用此方法推導出了載流導線循跡智能車解算跡線信息的三種數學模型,并給出了兩個結論,以輔助數學模型的運用。
地面上鋪設載流導線,通以一定頻率和幅值的周期性交變電流,作為引導智能車行進的跡線。用大電感作為傳感器,配以一定的電路,獲得相應的電壓。這是一種較新的循跡方式,在第五屆“飛思卡爾”杯全國大學生智能車競賽上出現。目前有兩種主要的跡線信息解算方法,一是通過整流濾波之后查表,使電壓與距離對應;二是用一排密集電感作為傳感器,靠近跡線的電感顯高電壓,遠離跡線的顯低電壓。由于大賽之前尚無精確的數學模型求解跡線信息,本文將試圖向這方面努力。
1.傳感器排布與賽道信息解算的數學模型
假設載流導線無限長直,電流為()it 。不妨假設電感為理想電感,即空間尺寸可忽略不計,電感鐵芯工作在線性區[1]。
空間一點某一方向上的磁感應強度為()Bt,由畢奧--薩伐爾定律[2]得![]() 其中K由空間位置決定,
其中K由空間位置決定,![]() 不妨將K稱為空間函數,電感不同的放置方式,對應不同的K。若跡線為無限長直的導線,則相同的電感放置方式下,K的表達式不變。
不妨將K稱為空間函數,電感不同的放置方式,對應不同的K。若跡線為無限長直的導線,則相同的電感放置方式下,K的表達式不變。

設()et為電感的開路感應電動勢,由法拉第電磁感應定律[3]得:
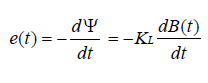 ,其中LK由電感的參數決定,是常數。
,其中LK由電感的參數決定,是常數。
將![]() 進行拉氏變換得
進行拉氏變換得![]() 其中
其中
將![]() 進行拉氏變換得
進行拉氏變換得![]() 其中
其中
將電感到A/D轉換之間的電路設計為線性時不變系統,設其傳遞函數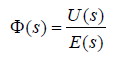 則
則
![]() 在小車起跑前測得
在小車起跑前測得
在小車起跑后測得
式(2)除以(1)得
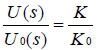
發現電路的傳遞函數和電流等與空間函數無關的項都被消去了。對于不同的電感排布方式,只要先得出空間函數K,然后運用該方法就能得出其對應的跡線信息解算表達式。這也正是本文要做的工作。為方便起見,將該方法稱為“法一”。





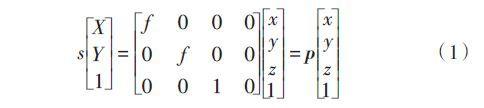








評論