數學界幾十年來的一個謎題，終于被解開了。

這個猜想和初等數論中經典的佩爾（Pell）方程：x²-d*y²=1有關。

（這里d是整數，求x、y也都是整數的解。）

在此之前，經典佩爾方程的整數解情況已得到證明：

當d≤0或d為某大于0的完全平方數時，該方程有唯一解：x=±1，y=0；當d>0且不是完全平方數時，該方程有無數組正整數解。

不過數學家們的探究精神一般不會止步于此。

有人提出將等號右邊的1變成-1，并將這個新的方程稱為負佩爾方程 （ II型佩爾方程），結果整數解的情況立刻變得復雜了許多。

時間撥到1993年，當時數學家彼得·史蒂文哈根（Peter Stevenhargen）提出了一個公式，對負佩爾方程的整數解情況給出一個精確的答案。

而這個猜想提出后的30年，數學界一直無法證明它的正確性。

但現如今，來自康考迪亞大學的卡羅·帕加諾（Carlo Pagano）和密歇根大學的皮特·科伊曼斯（Peter Koymans），終于給出了猜想的“正解”。

帕加諾的導師Hendrik Lenstra教授甚至對此評價說：

這個成果為數論的一個分支開辟了新篇章。

在介紹負佩爾方程之前，讓我們先來了解一下經典的佩爾方程從何而來。

佩爾方程，其實與佩爾完全無關。

這一理論最早由費馬（Pierre de Fermat）進行深入研究，由拉格朗日（Joseph-Louis Lagrange）給出解決方案，但后來因為被歐拉（Leonhard Euler）誤記為佩爾提出，就陰差陽錯的流傳下來。

它的具體形式為：x²-d*y²=1

當d是正整數且不是完全平方數，則存在無窮多個解。

舉個例子，數學史上有個經典的“阿基米德群牛問題”：

太陽神養了一群牛，這些牛有公有母，分白色、黑色、黃色和花色四種顏色，給定一系列條件，求解牛的總數有多少？各種顏色的牛分別是多少?

這個問題起一直以來吸引了很多數學家的興趣，最后經過一系列計算，被演化為求解一個佩爾方程：

x²-4729494*y²=1

2000年，倫斯查（Lenstra）完全解決了這個問題，他得出了阿基米德群牛問題的所有解：

不僅解的數量多，牛的最小數量也讓人驚呼：或許只有真·太陽神才能管理了。

不同于佩爾方程，負佩爾方程的整數解情況要復雜得多。

前文提到，負佩爾方程可表示為：x²-d*y²=-1；d為整數。

顯然，當d≤0，以及d為大于1的完全平方數時，方程無整數解。

此外，負佩爾方程的整數解復雜性還體現在：

負佩爾方程中的很多d值都無整數解。據已知規則得出，d不能是3、7、11、15的倍數等。

但除了這些值外，并不是其他的d值就一定有整數解。
例如當d=3時，x²–3*y²=-1，無論沿著數軸看多遠，都永遠找不到解。

但事實上，排除3、7、11、15的倍數后，并不是取其他的d值，負佩爾方程就一定有整數解。

給定d值后，首先需要求出負佩爾方程的基本解。

對負佩爾方程的求通解可使用這個公式：

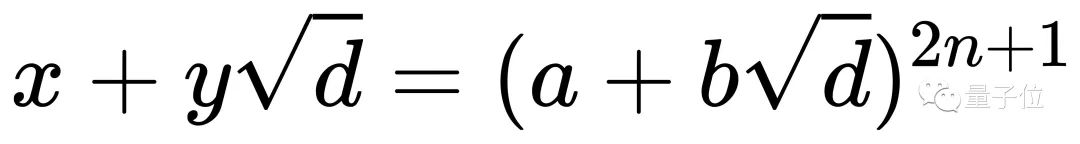
其中，這里的n為任意正整數；a和b則是負佩爾方程的基本解，并有如下等式：

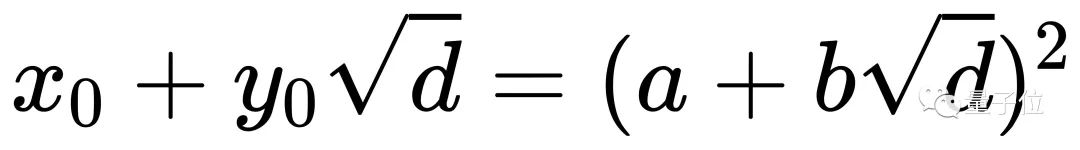
x₀和y₀就是經典佩爾方程的基本解。

更多與之相關的細節研究可參考論文：

最后，來看看這兩位證明這個30年前猜想的數學家們吧——

卡羅·帕加諾（Carlo Pagano），是加拿大康考迪亞大學的助理教授，主要研究方向是數論。

此前分別獲得了格拉斯哥大學和馬克斯·普朗克研究所的數學博士后學位，博士畢業于萊頓大學數學專業，導師是Hendrik Lenstra。

皮特·科伊曼斯（Peter Koymans），目前正在密歇根大學攻讀博士后，主要研究方向是數論及其周邊領域。

此前在馬克斯·普朗克數學研究所從事博士后研究，博士畢業于萊頓大學數學專業，導師是Jan-Hendrik Evertse和Peter Stevenhagen。

可以看出，兩人的學習軌跡有很多重合的部分，不僅如此，他們在研究生時期也是同學。

為了這項研究，兩人整整一年天天見面，每天在黑板上進行各種演算，互相完善對方提出來的想法，就連午餐時間都不放過，如果有人在獨處時有了新想法，就會隨時發****通知另一個人。

盡管非常有挑戰性，科伊曼斯卻在回憶起這段時間時說：“我們一起做這件事很有趣。”

參考鏈接：
[1]https://www.quantamagazine.org/ancient-equations-offer-new-look-at-number-groups-20220810/
[2]http://www.math.toronto.edu/~eknight/Pell.pdf
[3]https://zhuanlan.zhihu.com/p/365860557
[4]https://www.sites.google.com/view/carlopagano
[5]http://www-personal.umich.edu/~koymans/
[6]https://arxiv.org/abs/2201.13424

來源：量子位