的相位關系會發生轉換，從而判斷電機運行的方向。因此，根據這一特性，在FPGA中，用Vetilog語言編寫了一個實現正交編碼脈沖電路的功能的計數模塊。

同時，為了進一步消除光柵反饋信號可能產生的窄脈沖干擾信號，本控制器將轉換后的單端信號進一步濾波。主要過程是：在采集某一狀態信號時，利用比該狀態信號更高頻率的采樣時鐘對其進行多次重復采集，直到多次采集結果完全一致時才視為有效信號輸出。然后再將濾波過后的信號發送給正交編碼脈沖電路進行辨向和計數。

1.3 驅動控制器的控制方式

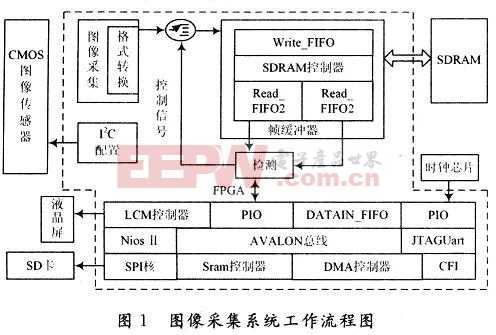
電機工作時，FPGA通過串口接收來自上位機發送的數據至Nios II處理器中，經過程序處理之后，得出電機運行的方式(步進、連續)、運行的距離等信息，NiosⅡ處理器通過控制DDS模塊的起停時間來控制驅動信號的有無進而控制電機的運動過程。電機運行時的位移和速度的實際信息可以從光柵編碼器的反饋信號中得出，計數器模塊計算出脈沖數的值發送給Nios II處理器，處理器通過具體的控制算法改變DDS輸出信號的幅值、頻率、相位從而對電機的運行狀態做出進一步的調整。這樣，一個完整的閉環控制系統就由一塊FPGA芯片實現了。

2 實驗分析

2.1 超聲電機速度穩定性研究

由于超聲電機在一定的頻率范圍內，它的速度隨著頻率的增大而減小，因此我們可以通過控制正弦信號的頻率來保證超聲電機速度的穩定性。

本實驗使用的直線超聲電機在33.8 kHz附近運行的比較穩定，所以選用33.8 kHz作為直線超聲電機的實驗頻率。首先研究直線超聲電機在不加入任何的控制算法時，它的速度穩定性，實驗結果如圖5所示。

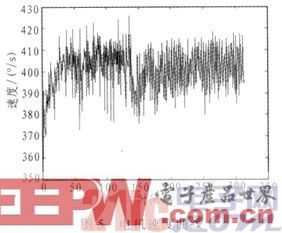
由上圖可以看出不加控制算法直接運行，超聲電機的速度不是很穩定。如果在Nios II處理器中加入一些控制算法去控制電機運行時的頻率，速度的穩定性會有顯著的改善。以增量式PID算法為例：

△u(k)=A1e(k)+A2e(k-1)+A3e(k-2)

u(k)是頻率，e(k)是第K次采樣時目標速度與當前速度的差值。通過上面的公式算出頻率的改變量，發送新的頻率控制字給DDS模塊，改變驅動信號的頻率，從而達到控制電機運行速度的效果。圖6為加入PID算法后電機的速度曲線。

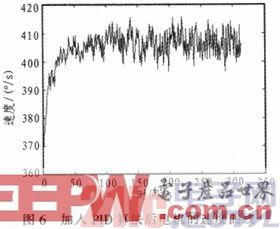
由此可見，引入控制算法的超聲電機驅動，電機的速度波動要遠遠的小于直線超聲電機在不引入算法時的波動。這很好的解決了直線超聲電機在運動過程中的速度穩定性問題。

2.2 定位精度測試

對一個單軸直線超聲電機運動平臺進行精確定位實驗。此精密運動平臺在脈沖寬度為3.5μs時有著比較穩定的輸出特性，步進距離大約在100 nm左右。使用“連續+步進”的方式進行精度測試，連續運動至預定目標處，然后利用微小步進進行調整。英國REN-ISHAW公司的XL-80激光干涉儀系統作為本次實驗的測定系統，將激光干涉儀顯示數據與定位距離進行比較。實驗表明，此超聲電機直線運動平臺的定位精度可以達到1μm。

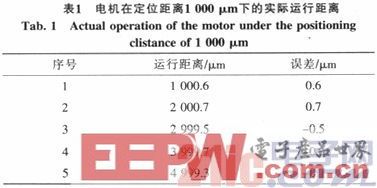
3 結論

文中利用SOPC技術，將波形發生模塊和微處理器模塊以及脈沖計數模塊巧妙地集成到一片FPGA內部，利用可編程邏輯的靈活性和Nios II的強大處理能力，實現了超聲電機驅動控制電路的設計。采用SOPC方案進行系統設計，充分利用FPGA的可編程性，整個開發過程變得靈活方便，在不改變任何外圍電路的情況下可以對系統進行軟硬件升級，延長系統的壽命周期，同時大大提升了系統的性能和系統的集成度，降低了系統的開發成本，這正是相對于其他方案的優勢，也符合當今科技的發展方向。