自適應在功率放大器非線性預失真中的應用
當μ較小時,τmse越大,收斂速度越慢,反之,收斂速度越快。
介于在μ的選擇上存在的一些矛盾,而在傳統自適應算法中μ為固定值,無論在穩定性及收斂速度方面都無法完全滿足系統的需求,本文采用了一種折中的方法,在信號處理初期,即25%emaxe(n)emax階段采用大步長的μ1,在0e(n)25%emax時采用小步長的μ2,這樣自適應濾波器在收斂速度與穩定性方面都得到一定程度的改善,加權系數迭代方程如下
,訓練器與預失真器的參數完全相同,理想情況下,=z,e(n)=0,根據前幾節介紹的自適應算法,更新預失真器的參數,使得e(n)趨向于0,從而達到線性放大的目的。
間接學習模型中的功放是一個Wiener模型,為一個線性時不變系統(LTI)與一個無記憶非線性模塊(NL)的串聯;預失真器為與Wiener模型具有逆特性的hammerstein模型。
用a1表示線性Wiener模型中LTI的系數,bk表示NL的系數,功率放大器的代數表達式為

3 系統仿真
本論文中的算法,通過matlab仿真平臺進行仿真,來檢測算法對帶外失真的改善程度,并且檢測了算法的收斂速度,輸入信號為WCDMA信號,預失真器中無記憶非線性部分的最高階取K=5,線性時不變系統部分長度取Q=7,功率放大器模型具有與其相同的多項式階數和記憶深度。
3.1 系統仿真
從實際功放中得到系數a1=14.9740+0.0519j,a3=-23.0954+4.9680j,a5=21.3936+0.4305j,通過分段變步長得到線性時不變系統的系數bk及無記憶非線性系統的系數cl的估值分別為

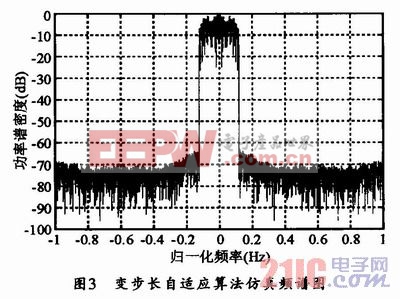
經過仿真后得到頻譜圖如圖3所示。本文引用地址:http://www.j9360.com/article/187315.htm






評論