摘要：為了實現大功率風力發電系統的恒功率控制，首先建立了基于直驅型PMSG風力發電系統的數學模型；其次，以功率偏差為控制器的輸入信號，設計了一種基于自抗擾算法的風力發電系統變槳距控制器。最后，在陣風疊加隨機風的作用下進行仿真研究。仿真結果表明，該控制器能夠有效地控制槳距角，可以實現額定風速以上時系統輸出功率的恒定。
關鍵詞：風力發電系統；恒功率；自抗擾；變槳距控制器

0 引言
風能作為一種清潔的可再生能源，越來越受到世界各國的重視，風力發電是風能最常見的利用形式。永磁同步風力發電系統不需要勵磁裝置，具有重量輕，效率高，可靠性好的優點。風力發電機組由最初的定槳距型發展到變槳距型，從轉速固定的變槳距型發展到目前技術最為先進的變速變槳距型，發電效率在顯著提高。特別是變速變槳距機組，其發電機中采用的變速恒頻技術提高了風力發電機組在低風速情況下的出力水平。采用永磁式發電機的直驅風力發電系統，無需外部提供勵磁電源，把永磁發電機變頻的交流電通過變頻器轉變為電網同頻的交流電，做到風力機與發電機的直接耦合，省去齒輪箱，大大減小了系統的運行噪聲，提高了可靠性，降低了系統成本，成為當前風力發電的研究熱點。直驅型PMSG風力發電系統的關鍵在于額定風速時的變槳距控制。變槳距風力發電機組的槳距參考值可由風速、電動機轉速和發電機輸出功率3個參數來獨立控制。文獻提出一種由槳距角大小來調節控制器增益的控制策略，即在原有PI控制系統中加入一個增益調整控制器。由于PI控制器缺少微分調節作用，系統的動態性能受到一定影響。文獻設計了模糊PID控制器對槳距角進行控制。輸入信號的誤差為e和誤差變化率為ec，運用模糊推理，自動實現對PID參數的最佳調整，以滿足不同時刻的e和ec對PID參數的自整定要求，從而得到槳距角變化目標的最佳調整。模糊PID控制器系統設計的核心為模糊控制規則設計，根據工程人員的實際操作經驗和技術知識得到。本文設計了一種基于自抗擾控制算法的控制器，該控制器的參數調整可不依賴于實際經驗，并能獲得更好的控制效果。仿真結果驗證了控制方法的有效性。

1 直驅型PMSG風力發電機組建模
1．1 風輪機模型
根據貝茲理論，風輪機產生的機械功率為：

式中：ρ為空氣密度；Rt為風力機風輪半徑；v為風速；Cp(λ，β)為風能轉換系數，是葉尖速比λ和槳葉節距角β的函數；葉尖速比λ為風輪葉尖線速度與風速之比，即；Ω1為風輪的機械角速度。
風輪機產生的風力矩：

式中：CΓ(λ，β)為轉矩系數，CΓ(λ，β)=Cp(λ，β)／λ。
在額定風速以下時，槳距角β為常值0。在額定風速以上，風能轉換系數滿足以下函數關系：

1．2 PMSG模型
在分析永磁同步電機的基本電磁關系時，假定永磁同步電機為理想電機，即滿足：
(1)忽略鐵心磁飽和的影響，不計渦流及磁滯損耗；
(2)永磁材料的電導率為零；
(3)轉子上沒有阻尼繞組；
(4)定子三相對稱，感應電動勢為正弦。
此時經過帕克變換后，在d-q軸坐標系下，PMSG的數學模型如下：

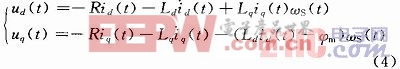
式中：R為定子電阻；ud(t)，uq(t)為d軸和q軸的定子電壓；Ld，Lq為d軸和q軸的定子電感；φm為永磁體產生的磁通；轉子旋轉的電角速度ωs(t)=p×Ωh(t)，d-q軸坐標系以電角速度ωs(t)隨轉子一同旋轉。
PMSG的電磁轉矩為：