2.2系統在時域范圍的算法

圖2電路所示的一階系統的傳遞函數為

式中UO為輸出信號;Ui為輸入信號;R為電阻;C為電容;t為時間。

利用MATLAB繪制單位階躍響應曲線如圖3。

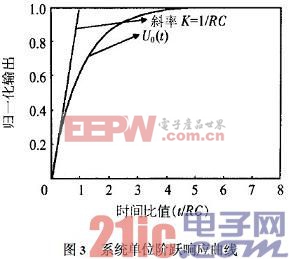
從圖3中可看出，該系統穩定、無振動。響應曲線的斜率為：

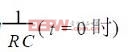
對式(2)進行變換得

從式(3)得，以lg[1-UO(t)]為縱坐標，t為橫坐標，可得出通過原點直線，從直線的斜率可求得常數RC的值，已知R則可得出C，從而得出壓力。

2.3模型識別

基于上述思想，若已知輸入、輸出信號，可通過曲線擬合及線性回歸法得出RC。對式(3)進行擬合，在擬合過程中，加入一定的白噪聲。若R=1000Ω，電容C=50pF，則擬合曲線如圖4所示。

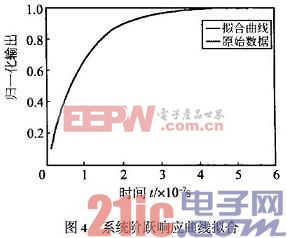
擬合參數最大時為5.037×10-8，最大相對誤差為0.78%。當溫度變化時，金屬鉑電阻值發生變化，在不同的溫度下擬合的電容值和溫度的關系如表1所示(加入1%的白噪聲)。

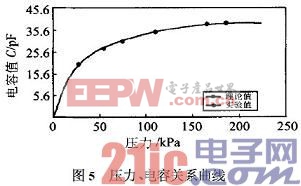
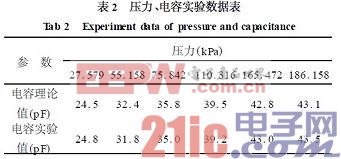
1可見，擬合的電容誤差小于1%。由此可見，在不同的時刻測得UO(t)，通過曲線擬合得出參數RC。再給電路加小信號直流電源，測出R值，即求得C，通過C值則可知被測環境的壓力。圖5為350℃時，不同的壓力所對應的電容的理論值和實驗值，從實驗數據(表2)可得，在測壓的過程中，利用模型識別的方法，誤差較小，其測壓誤差小于2%。

3結束語

基于模型識別技術的高溫微型壓力傳感器電路簡單、工藝成本較低、體積小、可批量生產、準確度高。該傳感器避免了電阻式高溫壓力傳感器的自補償電路在高溫環境下工作時熱靈敏度漂移引起的誤差，也避免了其它電容式高溫壓力傳感器非線性補償電路在高溫環境下工作。該傳感器適合在各種高溫環境下測量氣體或液體的壓力。